题目内容
函数f(x)=-|x-5|+2x-1的零点所在的区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:本题可求出相应区间端点的值,由连续函数根的存在性定理,端点值异号时,该区间内有根,得本题的解.
解答:
解:∵函数f(x)=-|x-5|+2x-1,
∴f(0)=-|0-5|+2-1=-
<0,
f(1)=-|1-5|+20=-3<0,
f(2)=-|2-5|+21=-1<0,
f(3)=-|3-5|+22=2>0,
f(4)=-|4-5|+23=7>0.
∵f(2)•f(3)<0,
∴函数f(x)=-|x-5|+2x-1的零点所在的区间是(2,3).
故选C.
∴f(0)=-|0-5|+2-1=-
| 9 |
| 2 |
f(1)=-|1-5|+20=-3<0,
f(2)=-|2-5|+21=-1<0,
f(3)=-|3-5|+22=2>0,
f(4)=-|4-5|+23=7>0.
∵f(2)•f(3)<0,
∴函数f(x)=-|x-5|+2x-1的零点所在的区间是(2,3).
故选C.
点评:本题考查了方程根的存在性定理,本题难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
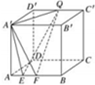 如图,正方体ABCD-A′B′C′D′的棱长为4,动点E,F在棱AB上,且EF=2,动点Q在棱D′C′上,则三棱锥A′-EFQ的体积( )
如图,正方体ABCD-A′B′C′D′的棱长为4,动点E,F在棱AB上,且EF=2,动点Q在棱D′C′上,则三棱锥A′-EFQ的体积( )| A、与点E,F位置有关 |
| B、与点Q位置有关 |
| C、与点E,F,Q位置有关 |
| D、与点E,F,Q位置均无关,是定值 |