Question

如果点P在以F为焦点的抛物线x²=2y上，且∠POF=60°（O为原点），那么△POF的面积是（　　）

• A、

  3

• B、

  3

  2

• C、

  3

  6

• D、

  3

  2

Answer 1

考点：双曲线的简单性质

专题：圆锥曲线的定义、性质与方程

分析：设点P在y轴右侧，由已知条件设P（x，

x2

2

），由∠POF=60°，能求出P点坐标，由此能求出|OP|，再由点到直线的距离公式，能求出点F到直线OP的距离，由此能求出△POF的面积．

解答： 解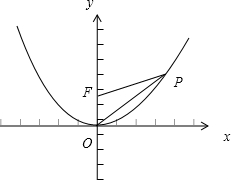：如图，设点P在y轴右侧，
∵点P在以F为焦点的抛物线x²=2y上，
∴F（0，

1

2

），设P（x，

x2

2

），
∵∠POF=60°，
∴k_PO=tan30°=

3

3

=

x2 2

x

，
解得x=

2 3

3

，∴P（

2 3

3

，

2

3

），
∴|OP|=

( 2 3 3 )2+( 2 3 )2

=

4

3

，
∵点F（0，

1

2

）到直线OP：y=

3

3

x的距离d=

| 1 2 |

( 3 3 )2+1

=

3

4

，
∴S_△POF=

1

2

×

4

3

×

3

4

=

3

6

．
故选：C．

点评：本题考查三角形面积的求法，是中档题，解题时要熟练掌握抛物线的简单性质，要注意点到直线的距离公式的应用．