题目内容
已知函数f(x)=sin(
x+
),x∈R.
(1)求函数f(x)的单调递减区间;
(2)求函数f(x)在区间[0,π]上的最大值及最小值;
(3)将函数y=sin(
x+
)的图象作怎样的变换可得到y=sinx的图象?
| 1 |
| 2 |
| π |
| 3 |
(1)求函数f(x)的单调递减区间;
(2)求函数f(x)在区间[0,π]上的最大值及最小值;
(3)将函数y=sin(
| 1 |
| 2 |
| π |
| 3 |
考点:函数y=Asin(ωx+φ)的图象变换,正弦函数的定义域和值域,正弦函数的单调性
专题:计算题,三角函数的图像与性质
分析:(1)直接利用正弦函数的单调减区间求解函数f(x)的单调递减区间;
(2)题干x∈[0,π],求出函数的相位的范围,利用正弦函数的值域求解函数的最大值及最小值;
(3)利用三角函数的平移与实数变换将函数y=sin(
x+
)的图象可得到y=sinx的图象.
(2)题干x∈[0,π],求出函数的相位的范围,利用正弦函数的值域求解函数的最大值及最小值;
(3)利用三角函数的平移与实数变换将函数y=sin(
| 1 |
| 2 |
| π |
| 3 |
解答:
解:(1)令z=
x+
,则y=sinz,
y=sinz的单调递减区间为[2kπ+
,2kπ+
],k∈Z,
由2kπ+
≤
x+
≤2kπ+
,k∈Z,
得:4kπ+
≤x≤4kπ+
,k∈Z,
又z=
x+
在R上为增函数,故原函数的单调递减区间为:
[4kπ+
,4kπ+
]k∈Z,
(2)令z=
x+
,则y=sinz,z∈[
,
].
当z=
,即x=
时,f(x)有最大值f(
)=1,
当z=
,即x=π时,f(x)有最小值f(π)=
;…(8分)
(3)法一:将y=sin(
x+
)的图象的横坐标变为原来的
,再向右平移
个单位.(12分)
法二:将y=sin(
x+
)的图象向右平移
个单位,再将横坐标变为原来的
.(12分)
| 1 |
| 2 |
| π |
| 3 |
y=sinz的单调递减区间为[2kπ+
| π |
| 2 |
| 3π |
| 2 |
由2kπ+
| π |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
得:4kπ+
| π |
| 3 |
| 7π |
| 3 |
又z=
| 1 |
| 2 |
| π |
| 3 |
[4kπ+
| π |
| 3 |
| 7π |
| 3 |
(2)令z=
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
当z=
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
当z=
| 5π |
| 6 |
| 1 |
| 2 |
(3)法一:将y=sin(
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
法二:将y=sin(
| 1 |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
点评:本题考查函数y=Asin(ωx+φ)的图象变换,正弦函数的单调性以及最值的求法,考查逻辑思维能力以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果点P在以F为焦点的抛物线x2=2y上,且∠POF=60°(O为原点),那么△POF的面积是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
抛物线y2=4x上的点M(x0,y0)到焦点F的距离为5,则x0的值为( )
| A、1 | B、3 | C、4 | D、5 |
 坚持锻炼一小时,健康成长每一天.某校为调查高中学生在校参加体育活动的时间,随机抽取了100名高中学生进行调查,其中女学生有55名.上面是根据调查结果绘制的学生日均体育锻炼时间的频率分布直方图:
坚持锻炼一小时,健康成长每一天.某校为调查高中学生在校参加体育活动的时间,随机抽取了100名高中学生进行调查,其中女学生有55名.上面是根据调查结果绘制的学生日均体育锻炼时间的频率分布直方图: 如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=4,E、F、G分别是PC、PD、BC的中点.
如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=4,E、F、G分别是PC、PD、BC的中点.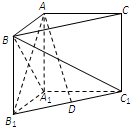 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.