题目内容
点P（2，5）与圆x2+y2=24的位置关系是（ ）
| A、在圆外 | B、在圆内 |
| C、在圆上 | D、不确定 |
考点：点与圆的位置关系
专题：直线与圆
分析：点P到圆心的距离大于半径?点在圆外；点P到圆心的距离等于半径?点在圆上；点P到圆心的距离小于半径?点到圆内．
解答：
解：圆x2+y2=24的圆心O（0，0），半径r=2
，
∵点P（2，5）与圆心O（0，0）的距离：
|OP|=
=
＞r=2
，
∴点P在圆外．
故选：A．
| 6 |
∵点P（2，5）与圆心O（0，0）的距离：
|OP|=
| 22+52 |
| 29 |
| 6 |
∴点P在圆外．
故选：A．
点评：本题考查点与圆的位置关系的判断，是基础题，由点到圆心的距离和圆半径的大小关系进行判断．
练习册系列答案
相关题目
(x-
)4的展开式中常数项为（ ）
| 1 |
| 2x |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
如果点P在以F为焦点的抛物线x2=2y上，且∠POF=60°（O为原点），那么△POF的面积是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知椭圆
+y2=1，则该椭圆的离心率为（ ）
| x2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
A={x|x2≥4}，B={x|2x=
}，则A∩B=（ ）
| 1 |
| 4 |
| A、{2} |
| B、（-∞，-2] |
| C、[2，+∞） |
| D、{-2} |
长方体共一顶点的三条棱长分别为
，
，2，则这个长方体外接球的体积为（ ）
| 2 |
| 3 |
A、
| ||||
B、
| ||||
| C、3π | ||||
D、
|
抛物线y2=4x上的点M（x0，y0）到焦点F的距离为5，则x0的值为（ ）
| A、1 | B、3 | C、4 | D、5 |
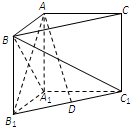如图，在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=AA1．