题目内容
 为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数次测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数次测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?
(3)在这次测试中,估计学生跳绳次数的众数和中位数、平均数各是多少?
考点:极差、方差与标准差,频率分布直方图,众数、中位数、平均数
专题:计算题,概率与统计
分析:(1)根据各个小矩形的面积之比,求出第二组的频率,再根据所给的频数,求出样本容量;
(2)从频率分步直方图中求出次数大于110以上的频率,由此估计高一全体学生的达标率;
(3)这组数据的众数是最高的小长方形的底边中点的横坐标,
中位数是把频率分布直方图分成两个相等部分的位置,
平均数是各小长方形底边中点的横坐标与对应频率的乘积的和.
(2)从频率分步直方图中求出次数大于110以上的频率,由此估计高一全体学生的达标率;
(3)这组数据的众数是最高的小长方形的底边中点的横坐标,
中位数是把频率分布直方图分成两个相等部分的位置,
平均数是各小长方形底边中点的横坐标与对应频率的乘积的和.
解答:
解:(1)∵各小长方形面积之比为2:4:17:15:9:3,
∴第二小组的频率是
=0.08;
∵第二小组频数为12,
∴样本容量是
=150;
(2)次数在110以上(含110次)的频率为
1-
-
=1-0.04-0.08=0.88,
∴估计该学校全体高一学生的达标率是0.88;
(3)根据频率分布直方图得,众数是
=115;
中位数落在的位置是刚好把频率分步直方图分成两个相等的部分的位置,是120+
≈121;
平均数是
=95×
+105×
+115×
+125×
+135×
+145×
=121.8≈122.
∴第二小组的频率是
| 4 |
| 2+4+17+15+9+3 |
∵第二小组频数为12,
∴样本容量是
| 12 |
| 0.08 |
(2)次数在110以上(含110次)的频率为
1-
| 2 |
| 2+4+17+15+9+3 |
| 4 |
| 2+4+17+15+9+3 |
∴估计该学校全体高一学生的达标率是0.88;
(3)根据频率分布直方图得,众数是
| 110+120 |
| 2 |
中位数落在的位置是刚好把频率分步直方图分成两个相等的部分的位置,是120+
| 6 |
| 4.5 |
平均数是
. |
| x |
| 2 |
| 50 |
| 4 |
| 50 |
| 17 |
| 50 |
| 15 |
| 50 |
| 9 |
| 50 |
| 3 |
| 50 |
点评:本题考查了利用频率分布直方图求数据的频率、样本容量、众数、中位数、平均数等知识,也考查了一定的计算能力,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
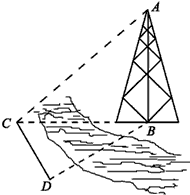 如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在点C处测得塔顶A的仰角为60°,求塔高AB.
如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在点C处测得塔顶A的仰角为60°,求塔高AB.