题目内容
已知函数f(x)=loga
(a>0,a≠1).
(1)求函数f(x)的定义域;
(2)讨论f(x)在(1,+∞)上的单调性,并用定义证明;
(3)令g(x)=1+logax,当[m,n]?(1,+∞)(m<n)时,f(x)在[m,n]上的值域是[g(n),g(m)],求实数a的取值范围.
| x-1 |
| x+1 |
(1)求函数f(x)的定义域;
(2)讨论f(x)在(1,+∞)上的单调性,并用定义证明;
(3)令g(x)=1+logax,当[m,n]?(1,+∞)(m<n)时,f(x)在[m,n]上的值域是[g(n),g(m)],求实数a的取值范围.
考点:函数单调性的判断与证明,函数的定义域及其求法,函数的值域
专题:函数的性质及应用
分析:(1)先求函数的定义域,(2)然后利用定义法求证函数的单调性,(3)利用函数的单调性和函数的值域得方程,利用对数的性质解方程即可得实数a的取值范围.
解答:
(本小题满分14分)
解:(1)由题意得
>0,其定义域是(-∞,-1)∪(1,+∞)----------------(2分)
(2)当0<a<1时,f(x)在(1,+∞)上是减函数;
当a>1时,f(x)在(1,+∞)上是增函数;----------------(4分)
证明:在(1,+∞)上任取x1,x2,设x1<x2,
-
=
因为1<x1<x2,x1-x2<0
-
=
<0,
即
<
----------------(6分)
当0<a<1时,loga
>loga
,
即f(x1)>f(x2),所以f(x)在(1,+∞)上是减函数;
当a>1时,loga
<loga
,
即f(x1)<f(x2),所以f(x)在(1,+∞)上是增函数;-----------(9分)
(3)由已知得g(n)<g(m),故0<a<1,f(x)在(1,+∞)上是减函数;
,由loga
=1+logax-----------(11分)
得
=ax,即ax2+(a-1)x+1=0的两根均大于1
即
,解得0<a<3-2
-----------(14分)
解:(1)由题意得
| x-1 |
| x+1 |
(2)当0<a<1时,f(x)在(1,+∞)上是减函数;
当a>1时,f(x)在(1,+∞)上是增函数;----------------(4分)
证明:在(1,+∞)上任取x1,x2,设x1<x2,
| x1-1 |
| x1+1 |
| x2-1 |
| x2+1 |
| 2(x1-x2) |
| (x1+1)(x2+1) |
因为1<x1<x2,x1-x2<0
| x1-1 |
| x1+1 |
| x2-1 |
| x2+1 |
| 2(x1-x2) |
| (x1+1)(x2+1) |
即
| x1-1 |
| x1+1 |
| x2-1 |
| x2+1 |
当0<a<1时,loga
| x1-1 |
| x1+1 |
| x2-1 |
| x2+1 |
即f(x1)>f(x2),所以f(x)在(1,+∞)上是减函数;
当a>1时,loga
| x1-1 |
| x1+1 |
| x2-1 |
| x2+1 |
即f(x1)<f(x2),所以f(x)在(1,+∞)上是增函数;-----------(9分)
(3)由已知得g(n)<g(m),故0<a<1,f(x)在(1,+∞)上是减函数;
|
| x-1 |
| x+1 |
得
| x-1 |
| x+1 |
即
|
| 2 |
点评:本题考查函数的定义域值域和单调性,属于函数性质的综合应用,属于中档题目,应熟练掌握函数的性质,函数为高考中的热点.

练习册系列答案
相关题目
给出下列四个命题,其中不正确的是( )
| A、函数y=tanx是增函数 | ||
B、y=|sin2x|的最小正周期是
| ||
C、函数y=cosx在[2kπ+π,2kπ+
| ||
D、函数y=tan(x+
|
线段AB长为2a,两端点A,B分别在一个直二面角的两个面内,且AB与两个面所成的角分别为30°和45°,设A,B两点在二面角棱上的射影分别为A′,B′,则A′B′的长为( )
A、
| ||||
B、
| ||||
| C、a | ||||
| D、2a |
设
、
是平面内的两个向量,则有( )
| e1 |
| e2 |
A、
| ||||||||||||
B、
| ||||||||||||
C、对同一平面内的任一向量
| ||||||||||||
D、若
|
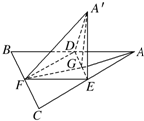 如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形(点A′∉平面ABC),则下列命题中正确的是
如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形(点A′∉平面ABC),则下列命题中正确的是