题目内容
函数y=4x2-
单调递增区间是( )
| 1 |
| x |
| A、(0,+∞) | ||
B、(-
| ||
C、(-
| ||
D、(-
|
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:求函数的定义域和导数,利用函数单调性和导数之间的关系即可得到结论.
解答:
解:函数的定义域伟{x|x≠0},函数的导数f′(x)=8x+
=
,
令f′(x)>0得8x3>-1,即x>-
且x≠0,
∴函数f(x)的单调递增区间为(-
,0),(0,+∞).
故选D.
| 1 |
| x2 |
| 8x3+1 |
| x2 |
令f′(x)>0得8x3>-1,即x>-
| 1 |
| 2 |
∴函数f(x)的单调递增区间为(-
| 1 |
| 2 |
故选D.
点评:考查利用导数求函数的单调区间,利用函数单调性和导数之间的关系是解决本题的关键.注意要先求函数的定义域.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
已知集合A={ 1,2,},B={x|ax-1=0},满足B⊆A的实数a组成集合C子集个数是( )
| A、4 个 |
| B、8 个 |
| C、16 个 |
| D、32个 |
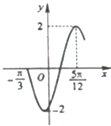
函数f(x)=2sin(ωx+φ)(ω>0,-
<φ<
)的部分图象如图,则ω,φ的值分别是( )
| π |
| 2 |
| π |
| 2 |

A、ω=1,φ=-
| ||
B、ω=1,φ=-
| ||
C、ω=2,φ=-
| ||
D、ω=2,φ=-
|
设i为虚数单位,复数Z的共轭复数为
,且(
+1)(1-i)=2i,则复数Z的模为( )
. |
| Z |
. |
| Z |
A、
| ||
| B、5 | ||
| C、-2-i | ||
| D、1 |
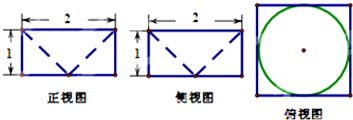
如图是一个空间几何体的三视图,则该几何体的体积为( )

A、4-
| ||
B、8-
| ||
C、4-
| ||
D、8-
|
已知全集U=R,集合A={(x,y)|y=
},B={x|0<x≤1},则(∁UA)∪B=( )
| x2-x |
| A、(0,1) |
| B、(0,1] |
| C、(-∞,0)∪(1,+∞) |
| D、∅ |
为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
下面的临界值供参考:
x2=
,其中n*1=n11+n22,n*2=n12+n21,n1*=n11+n12,n2*=n21+n22,n=n11+n22+n12+n21
下列结论正确的是( )
| 做不到“光盘” | 能做到“光盘” | 合计 | |
| 男 | 45 | 10 | 55 |
| 女 | 25 | 20 | 45 |
| 合计 | 70 | 30 | 100 |
x2=
| n(n11n22n12n21)2 |
| n1*n2*n*1n*2 |
| P(x2≥k) | 0.05 | 0.010 | 0.005 | 0.001 |
| K | 3.841 | 6.635 | 7.879 | 10.828 |
| A、有95%以上的把握认为“该市居民能否做到“光盘”与性别有关 |
| B、有99%以上的把握认为“该市居民能否做到“光盘”与性别有关 |
| C、有99.5%以上的把握认为“该市居民能否做到“光盘”与性别有关 |
| D、性别不同决定了能否做到“光盘” |
实数x,y满足
,则3x+y的最大值为( )
|
A、
| ||||||
B、3+
| ||||||
C、
| ||||||
| D、17 |