题目内容
过抛物线y2=2px(p>0)的焦点F作斜率为1的直线交抛物线于A,B两点,若线段|AB|=8,则p=
;过抛物线x2=2py(p>0)的焦点F作倾角为30°的直线,与抛物线分别交于A,B两点(A在y轴左侧),则
= .
;过抛物线x2=2py(p>0)的焦点F作倾角为30°的直线,与抛物线分别交于A,B两点(A在y轴左侧),则
| |AF| |
| |FB| |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设直线AB的方程与抛物线的方程联立,利用根与系数的关系可得x1+x2.再利用弦长公式|AB|=x1+x2+p,即可得到p;
解答:
解:抛物线y2=2px的焦点F(
,0),准线方程为x=-
∴直线AB的方程为y=x-
,
代入y2=2px可得x2-3px+
=0
∴xA+xB=3p,
由抛物线的定义可知,AB=AF+BF=xA+xB+p=4p=8
∴p=2;
设直线l的方程为:x=
(y-
),设A(x1,y1),B(x2,y2),
将直线方程代入抛物线方程,消去x可得12y2-20py+3p2=0,
解方程得y1=
,y2=
由抛物线的性质知,
=
=
.
故答案为:2,
.
| p |
| 2 |
| p |
| 2 |
∴直线AB的方程为y=x-
| p |
| 2 |
代入y2=2px可得x2-3px+
| p2 |
| 4 |
∴xA+xB=3p,
由抛物线的定义可知,AB=AF+BF=xA+xB+p=4p=8
∴p=2;
设直线l的方程为:x=
| 3 |
| p |
| 2 |
将直线方程代入抛物线方程,消去x可得12y2-20py+3p2=0,
解方程得y1=
| p |
| 6 |
| 3p |
| 2 |
由抛物线的性质知,
| |AF| |
| |FB| |
y1+
| ||
y2+
|
| 1 |
| 3 |
故答案为:2,
| 1 |
| 3 |
点评:本题考查了抛物线的定义、标准方程,以及简单性质的应用,考查直线与抛物线相交问题、焦点弦长问题、弦长公式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则通过该段公路的汽车中,时速在[60,80]的汽车所占比例的估计值为( )
200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则通过该段公路的汽车中,时速在[60,80]的汽车所占比例的估计值为( )| A、20% | B、40% |
| C、60% | D、80% |
函数y=4x2-
单调递增区间是( )
| 1 |
| x |
| A、(0,+∞) | ||
B、(-
| ||
C、(-
| ||
D、(-
|

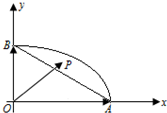 A,B是椭圆的右顶点及上顶点,由椭圆弧
A,B是椭圆的右顶点及上顶点,由椭圆弧