题目内容
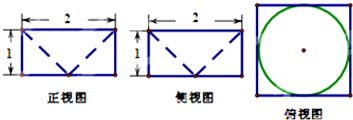
如图是一个空间几何体的三视图,则该几何体的体积为( )

A、4-
| ||
B、8-
| ||
C、4-
| ||
D、8-
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知中的三视图,可得该几何体是底面为一个正方形的长方体,挖掉一个圆锥所得,分别计算长方体和圆锥的体积,相减可得答案.
解答:
解:由已知中的三视图,可得该几何体是底面为一个正方形的长方体,挖掉一个圆锥所得,
长方体的体积为:2×2×1=4,
圆锥的体积为:
×π×12×1=
,
故组合体的体积V=4-
,
故选:A
长方体的体积为:2×2×1=4,
圆锥的体积为:
| 1 |
| 3 |
| π |
| 3 |
故组合体的体积V=4-
| π |
| 3 |
故选:A
点评:本题考查的知识点是由三视图求体积,其中分析出几何体的形状是解答的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
执行如图所示的程序框图,输出的结果为( )


| A、4094 | B、1022 |
| C、2046 | D、2048 |
执行如图所示的程序框图,如果输入的N是5,那么输出的p是( )


| A、24 | B、102 |
| C、120 | D、720 |
函数y=4x2-
单调递增区间是( )
| 1 |
| x |
| A、(0,+∞) | ||
B、(-
| ||
C、(-
| ||
D、(-
|
函数f(x)=sin(2x+
),x∈R的最小正周期为( )
| π |
| 4 |
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
sin89°cos14°-sin1°cos76°=( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
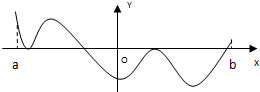 函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值点( )
函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值点( )| A、1个 | B、2个 | C、3个 | D、4个 |
10个三好学生名额,分给甲、乙、丙三个班,每班至少一名,共有( )种方法.
| A、24 | B、48 | C、36 | D、72 |