题目内容
实数x,y满足
,则3x+y的最大值为( )
|
A、
| ||||||
B、3+
| ||||||
C、
| ||||||
| D、17 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,根据z的几何意义,利用数形结合即可得到最大值.
解答:
解:∵
,∴
,
不等式组对应的平面区域如图:
设z=3x+y得y=-3x+z,
平移直线y=-3x+z,则由图象可知当直线y=-3x+z经过点A时直线y=-3x+z的截距最大,此时z最大,
由
,解得
,
即A(4,5),此时3x+y的最大值12+5=17,
故选:D
|
|

不等式组对应的平面区域如图:
设z=3x+y得y=-3x+z,
平移直线y=-3x+z,则由图象可知当直线y=-3x+z经过点A时直线y=-3x+z的截距最大,此时z最大,
由
|
|
即A(4,5),此时3x+y的最大值12+5=17,
故选:D
点评:本题主要考查线性规划的应用,根据z的几何意义,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
函数y=4x2-
单调递增区间是( )
| 1 |
| x |
| A、(0,+∞) | ||
B、(-
| ||
C、(-
| ||
D、(-
|
已知f(x)的定义域为R,则p:?x∈R,(f(x)+f(-x))•(f(x)-f(-x))=0是q:f(x)为奇函数或偶函数的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知一个几何体的三视图如图所示,则该几何体的体积为( )
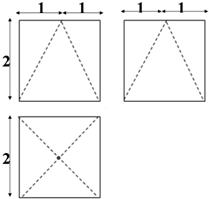

| A、8 | ||
B、
| ||
C、
| ||
| D、4 |
设a>0,b>0,且不等式
+
+
≥0恒成立.则实数k的最小值等于( )
| 1 |
| a |
| 1 |
| b |
| k |
| a+b |
| A、4 | B、0 | C、-2 | D、-4 |
10个三好学生名额,分给甲、乙、丙三个班,每班至少一名,共有( )种方法.
| A、24 | B、48 | C、36 | D、72 |
在等差数列{an}中,若a3+a8=24,则S10的值为( )
| A、20 | B、60 | C、90 | D、120 |