题目内容

7．现有甲，乙，丙，丁四位同学课余参加巴蜀爱心社和巴蜀文学风的活动，每人参加且只能参加一个社团的活动，并且参加每个社团都是等可能的．
（1）求巴蜀爱心社和巴蜀文学风都至少有1人参加的概率；
（2）求甲，乙在同一个社团，丙，丁不在同一个社团的概率．

分析 甲、乙、丙、丁4个学生课余参加巴蜀爱心社和巴蜀文学风的情况如下共有16种情形，即有16个基本事件，分别找出满足条件的基本事件，根据概率公式计算即可．

解答 解：甲、乙、丙、丁4个学生课余参加巴蜀爱心社和巴蜀文学风的情况如下共有16种情形，即有16个基本事件．
（1）巴蜀爱心社和巴蜀文学风没有人参加的基本事件有2个，概率为$\frac{14}{16}$=$\frac{7}{8}$；
（2）甲、乙同在一个社团，且丙、丁不同在一个社团的基本事件有4个，概率为$\frac{4}{16}$=$\frac{1}{4}$．

点评 本题考查古典概型计算，属于基础题．

练习册系列答案
相关题目
17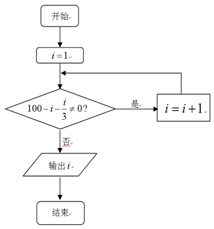．《孙子算经》中有道算术题：“今有百鹿人城，家取一鹿不尽，又三
家共一鹿适尽，问城中家几何？”意思是有100头鹿，每户分1头还有
剩余；再每3户共分1头，正好分完，问共有多少户人家？设计框图如
下，则输出的值是（　　）
A．74B．75C．76D．77
18．已知函数f（x）=|2x-a|-|x|，a∈R
（1）当a=2时，解关于的不等式f（x）＞1；
（2）若f（x）≥4-|2x+a|-|x|对?x∈R恒成立，求实数的取值范围．
15．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点（1，$\frac{\sqrt{3}}{2}$），离心率为$\frac{\sqrt{3}}{2}$，点A为椭圆C的右顶点，直线l与椭圆相交于不同于点A的两个点P（x1，y1），Q（x2，y2）．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）当$\overrightarrow{AP}$⊥$\overrightarrow{AQ}$=0时，求△OPQ面积的最大值．
2．已知圆C：x2+y2-2x-4y+1=0上存在两点关于直线l：x+my+1=0对称，经过点M（m，m）作圆C的切线，切点为P，则m=-1；|MP|=3..
12．等比数列{an}的各项均为正数，且a1+2a2=4，a42=4a3a7，则a5=（　　）
A．$\frac{1}{8}$B．$\frac{1}{16}$C．20D．40
3．若函数f（x）为奇函数，且在（0，+∞）上是增函数，又f（-3）=0，则不等式x[f（-x）-f（x）]＜0的解集为（　　）
A．（-∞，-3）∪（0，3）B．（-2，0）∪（3，+∞）C．（-3，3）D．（-∞，-3）∪（3，+∞）
20．已知函数f（x）=$\frac{lnx}{x}$，关于x的不等式f2（x）+af（x）＞0只有一个整数解，则实数a的取值范围是（　　）
A．（-$\frac{ln3}{3}$，-$\frac{ln2}{2}$]B．（-$\frac{1}{e}$，-$\frac{ln2}{2}$]C．[$\frac{ln2}{2}$，-$\frac{ln3}{3}$]D．[$\frac{ln2}{2}$，$\frac{1}{e}$）
1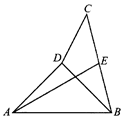．将正方形ABCD沿对角线BD折成直二面角后的图形如图所示，若E为线段BC的中点，则直线AE与平面ABD所成角的余弦为（　　）
A．$\frac{1}{4}$B．$\frac{{\sqrt{6}}}{6}$C．$\frac{{\sqrt{30}}}{6}$D．$\frac{{\sqrt{15}}}{4}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网