题目内容

12．等比数列{an}的各项均为正数，且a1+2a2=4，a42=4a3a7，则a5=（　　）
A．$\frac{1}{8}$B．$\frac{1}{16}$C．20D．40

分析 根据通项公式列方程组解出首项和公比，再计算a5．

解答 解：设公比为q，则q＞0，
由题意得：$\left\{\begin{array}{l}{{a}_{1}+2{a}_{1}q=4}\\{{{a}_{1}}^{2}{q}^{6}=4{a}_{1}{q}^{2}{a}_{1}{q}^{6}}\end{array}\right.$，
解得$\left\{\begin{array}{l}{{a}_{1}=2}\\{q=\frac{1}{2}}\end{array}\right.$，∴a5=2×$（\frac{1}{2}）^{4}$=$\frac{1}{8}$，
故选A．

点评 本题考查了等比数列的通项公式，属于基础题．

练习册系列答案
相关题目
2．已知函数f（x）=Msin（ωx+φ）$（M＞0，|φ|＜\frac{π}{2}，0＜ω＜3）$图象上的一个最高点为$（\frac{2}{3}π，2）$，函数f（x）图象与y轴交点为（0，1）．
（Ⅰ）求M，ω，φ的值；
（Ⅱ）在△ABC中，内角A，B，C所对的边分别是a，b，c，满足（2a-c）cosB=bcosC，求函数f（A）的取值范围．
3．将曲线的参数方程$\left\{\begin{array}{l}x=4\sqrt{t}+\frac{1}{{\sqrt{t}}}\\ y=4\sqrt{t}-\frac{1}{{\sqrt{t}}}\end{array}\right.（t$为参数）化为普通方程为（　　）
A．x2+y2=16B．x2+y2=16（x≥4）C．x2-y2=16D．x2-y2=16（x≥4）
20．已知某中学高三文科班学生共有800人参加了数学与地理的水平测试，学校决定利用随机数表法从中抽取100人进行成绩抽样调查．抽取的100人的数学与地理的水平测试成绩如下表：
人数数学
优秀良好及格
地理优秀7205
良好9186
及格a4b
成绩分为优秀、良好、及格三个等级；横向，纵向分别表示地理成绩与数学成绩，例如：表中数学成绩为良好的共有20+18+4=42人．
（1）在该样本中，数学成绩优秀率是30%，求a，b的值；
（2）在地理成绩及格的学生中，已知a≥10，b≥7，求数学成绩优秀的人数比及格的人数少的概率．
7．现有甲，乙，丙，丁四位同学课余参加巴蜀爱心社和巴蜀文学风的活动，每人参加且只能参加一个社团的活动，并且参加每个社团都是等可能的．
（1）求巴蜀爱心社和巴蜀文学风都至少有1人参加的概率；
（2）求甲，乙在同一个社团，丙，丁不在同一个社团的概率．
1．函数y=log${\;}_{\frac{1}{2}}$（3x-a）的定义域是（$\frac{2}{3}$，+∞），则a=2．
8．已知f′（x）为函数f（x）的导函数，且$f（x）=\frac{1}{2}{x^2}-f（0）+f'（1）{e^{x-1}}$，若$g（x）=f（x）-\frac{1}{2}{x^2}+x$，则方程$g（\frac{x^2}{a}-x）-x=0$有且仅有一个根时，a的取值范围是（　　）
A．[1，+∞）B．（-∞，1]C．（0，1]D．（-∞，0）∪{1}
5．执行如图的程序框图，如果输入的a=6，b=4，那么输出的s的值为（　　）
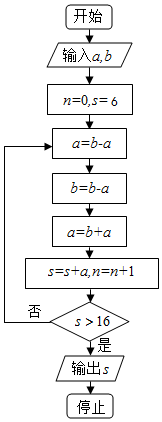
A．17B．22C．18D．20
6．“${（\frac{1}{3}）^a}＜{（\frac{1}{3}）^b}$”是“log2a＞log2b”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网