题目内容
20.已知函数f(x)=$\frac{lnx}{x}$,关于x的不等式f2(x)+af(x)>0只有一个整数解,则实数a的取值范围是( )| A. | (-$\frac{ln3}{3}$,-$\frac{ln2}{2}$] | B. | (-$\frac{1}{e}$,-$\frac{ln2}{2}$] | C. | [$\frac{ln2}{2}$,-$\frac{ln3}{3}$] | D. | [$\frac{ln2}{2}$,$\frac{1}{e}$) |
分析 利用导数,求出f(x)的单调性,通过讨论a的符号,结合图象,解关于f(x)的不等式结合不等式解的个数,求出a的范围即可.
解答 解:(1)f′(x)=$\frac{1-lnx}{{x}^{2}}$,令f′(x)>0,解得:0<x<e,
令f′(x)<0,解得:x>e,
∴f(x)的递增区间为(0,e),递减区间为(e,+∞),故f(x)的最大值是f(e)=$\frac{1}{e}$.
x→+∞时,f(x)→0,x→0时,x→-∞,f(1)=0,故在(0,1)时,f(x)<0,在(1,+∞)时,f(x)>0,
函数f(x)的图象如下: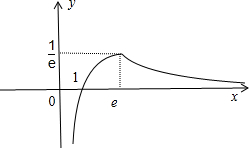
①a<0时,由不等式f2(x)+af(x)>0得f(x)>-a>0或f(x)<0,
而f(x)<0的解集为(0,1)无整数解,f(x)>-a>0的解集整数解一个,
∵f(x)在(0,e)递增,在(e,+∞)递减,
而2<e<3,f(2)=f(4)<f(3),这一个正整数只能为3,
∴f(2)≤-a<f(3),∴-$\frac{ln3}{3}$<a$≤-\frac{ln2}{2}$
②a=0时,由不等式f2(x)+af(x)>0,得f(x)≠0,解集为(0,1)∪(1,+∞),
整数解有无数多个,不合题意;
③a>0时,由不等式f2(x)+af(x)>0,得f(x)>0或f(x)<-a<0,
∵f(x)<-a<0的解集为(0,1)无整数解,而f(x)>0的解集为(1,+∞),整数解有无数多个,不合题意;
综上,故选:A
点评 题考查了函数图象及单调性,考查导数的应用以及分类讨论思想,转化思想、数形结合思想,属于中档题.

练习册系列答案
相关题目
8.已知f′(x)为函数f(x)的导函数,且$f(x)=\frac{1}{2}{x^2}-f(0)+f'(1){e^{x-1}}$,若$g(x)=f(x)-\frac{1}{2}{x^2}+x$,则方程$g(\frac{x^2}{a}-x)-x=0$有且仅有一个根时,a的取值范围是( )
| A. | [1,+∞) | B. | (-∞,1] | C. | (0,1] | D. | (-∞,0)∪{1} |
15.过抛物线C:y2=2px(p>0)的焦点F作斜率为$\frac{4}{3}$的直线l与C及其准线分别相交于A、B、D三点,则$\frac{|AD|}{|BD|}$的值为( )
| A. | 2或$\frac{1}{2}$ | B. | 3或$\frac{1}{3}$ | C. | 1 | D. | 4或$\frac{1}{4}$ |
5.执行如图的程序框图,如果输入的a=6,b=4,那么输出的s的值为( )
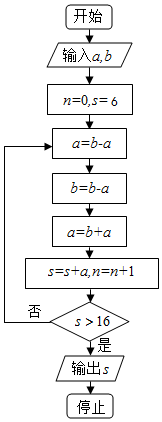

| A. | 17 | B. | 22 | C. | 18 | D. | 20 |
12.已知f(x)=1+(1+x)+(1+x)2+(1+x)3+…+(1+x)n,则f'(0)=( )
| A. | n | B. | n-1 | C. | $\frac{n(n-1)}{2}$ | D. | $\frac{1}{2}$n(n+1) |
10.若m=0.52,n=20.5,p=log20.5,则( )
| A. | n>m>p | B. | n>p>m | C. | m>n>p | D. | p>n>m |
