题目内容
7.设$|{\overrightarrow a}|=2$,$|{\overrightarrow b}|=1$,若$\overrightarrow a与\overrightarrow b的夹角为\frac{π}{3}$,则$\overrightarrow a•({\overrightarrow a+\overrightarrow b})$的值等于( )| A. | 4 | B. | 5 | C. | 6 | D. | $4+\sqrt{3}$ |
分析 根据平面向量数量积的定义,计算$\overrightarrow a•({\overrightarrow a+\overrightarrow b})$的值即可.
解答 解:$|{\overrightarrow a}|=2$,$|{\overrightarrow b}|=1$,$\overrightarrow a与\overrightarrow b的夹角为\frac{π}{3}$,
则$\overrightarrow a•({\overrightarrow a+\overrightarrow b})$=${\overrightarrow{a}}^{2}$+$\overrightarrow{a}$•$\overrightarrow{b}$=22+2×1×cos$\frac{π}{3}$=4+1=5.
故选:B.
点评 本题考查了平面向量数量积的计算问题,是基础题.

练习册系列答案
相关题目
17.五本不同的书在书架上排成一排,其中甲,乙两本必须连排,而丙,丁两本不能连排,则不同的排法共( )
| A. | 12种 | B. | 20种 | C. | 24种 | D. | 48种 |
15.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左焦点为F,若点F关于直线$y=-\frac{1}{2}x$的对称点P在椭圆C上,则椭圆C的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{5}}}{3}$ |
2.已知全集U=R,集合$A=\left\{{y\left|{y={{(\frac{1}{2})}^x}+1}\right.}\right\}$,集合B={y|y=b,b∈R},若A∩B=∅,则b的取值范围是( )
| A. | b<0 | B. | b≤0 | C. | b<1 | D. | b≤1 |
12.某几何体的三视图如图所示,则该几何体的体积是( )
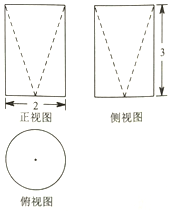

| A. | π | B. | 2π | C. | 3π | D. | 8π |
19.已知△ABC中,BC=1,A=120°,∠B=θ,记f(θ)=$\overrightarrow{BC}•\overrightarrow{AC}$,
①求f(θ)关于θ的表达式.
②求f(θ)的值域.
①求f(θ)关于θ的表达式.
②求f(θ)的值域.
16.某几何体的三视图如图所示,则该几何体的体积是( )


| A. | $\frac{2π}{3}$ | B. | π | C. | 2π | D. | 3π |