题目内容
2.已知全集U=R,集合$A=\left\{{y\left|{y={{(\frac{1}{2})}^x}+1}\right.}\right\}$,集合B={y|y=b,b∈R},若A∩B=∅,则b的取值范围是( )| A. | b<0 | B. | b≤0 | C. | b<1 | D. | b≤1 |
分析 先分别求出集合A={y|y>1},集合B={y|y=b,b∈R},由此利用A∩B=∅,能求出b的取值范围.
解答 解:∵全集U=R,集合$A=\left\{{y\left|{y={{(\frac{1}{2})}^x}+1}\right.}\right\}$={y|y>1},
集合B={y|y=b,b∈R},A∩B=∅,
∴b≤1
∴b的取值范围是{b|b≤1}.
故选:D.
点评 本题考查交集的求法,是基础题,解题时要认真审题,注意交集定义的合理运用.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
7.设$|{\overrightarrow a}|=2$,$|{\overrightarrow b}|=1$,若$\overrightarrow a与\overrightarrow b的夹角为\frac{π}{3}$,则$\overrightarrow a•({\overrightarrow a+\overrightarrow b})$的值等于( )
| A. | 4 | B. | 5 | C. | 6 | D. | $4+\sqrt{3}$ |
14.tan40°+tan80°-$\sqrt{3}$tan40°tan80°的值是( )
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
11.“a=-1”是“直线ax+3y+3=0与直线x+(a-2)y-3=0平行”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
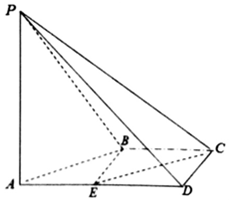 如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD,E为AD的中点,异面直线AP与CD所成的角为90°.
如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD,E为AD的中点,异面直线AP与CD所成的角为90°. 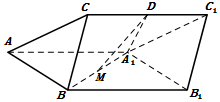 如图,三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.
如图,三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.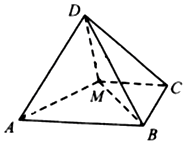 如图,四棱锥D-ABCM中,AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如图,四棱锥D-ABCM中,AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.