题目内容
19.已知△ABC中,BC=1,A=120°,∠B=θ,记f(θ)=$\overrightarrow{BC}•\overrightarrow{AC}$,①求f(θ)关于θ的表达式.
②求f(θ)的值域.
分析 ①利用正弦定理求出AC的值,再利用平面向量的数量积计算f(θ)=$\overrightarrow{BC}•\overrightarrow{AC}$;
②由①化简f(x),利用θ的取值范围,求出正弦函数的取值范围即可.
解答 解:①如图所示,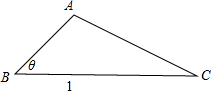
△ABC中,BC=1,A=120°,∠B=θ,
由正弦定理得,$\frac{AC}{sinθ}$=$\frac{BC}{sinA}$=$\frac{1}{sin120°}$=$\frac{2}{\sqrt{3}}$
∴AC=$\frac{2sinθ}{\sqrt{3}}$
∴f(θ)=$\overrightarrow{BC}•\overrightarrow{AC}$
=1×$\frac{2sinθ}{\sqrt{3}}$×cos(180°-120°-θ)
=$\frac{2sinθ}{\sqrt{3}}$×(cos60°cosθ+sin60°sinθ)
=$\frac{1}{\sqrt{3}}$sinθcosθ+sin2θ
=$\frac{1}{2\sqrt{3}}$sin2θ-$\frac{1}{2}$cos2θ+$\frac{1}{2}$
=$\frac{1}{\sqrt{3}}$($\frac{1}{2}$sin2θ-$\frac{\sqrt{3}}{2}$cos2θ)+$\frac{1}{2}$
=$\frac{\sqrt{3}}{3}$sin(2θ-60°)+$\frac{1}{2}$,其中θ∈(0°,60°);
②由①知,θ∈(0°,60°),
∴2θ∈(0°,120°),
∴2θ-60°∈(-60°,60°),
∴sin(2θ-60°)∈(-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$)
∴$\frac{\sqrt{3}}{3}$sin(2θ-60°)+$\frac{1}{2}$∈(0,1);
即f(θ)的值域是(0,1).
点评 本题考查了平面向量的数量积运算与三角函数的图象与性质的应用问题,是综合题.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
| A. | 4 | B. | 5 | C. | 6 | D. | $4+\sqrt{3}$ |
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
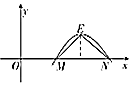 已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的导函数的部分图象如图所示,E是最高点,且△MNE是边长为1的正三角形,那么$f({\frac{1}{3}})$=( )
已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的导函数的部分图象如图所示,E是最高点,且△MNE是边长为1的正三角形,那么$f({\frac{1}{3}})$=( )| A. | $-\frac{{\sqrt{3}}}{2π}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $-\frac{3}{4π}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
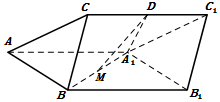 如图,三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.
如图,三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.