题目内容
17.命题“?x>2,都有x2>2”的否定是?x0>2,x02≤2.分析 直接利用全称命题的否定是特称命题写出结果即可.
解答 解:命题“?x>2,x2>2”是全称命题,其否定是:?x0>2,x02≤2.
故答案为:?x0>2,x02≤2.
点评 本题考查命题的否定,全称命题与特称命题的否定关系,基本知识的考查.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
7.设$|{\overrightarrow a}|=2$,$|{\overrightarrow b}|=1$,若$\overrightarrow a与\overrightarrow b的夹角为\frac{π}{3}$,则$\overrightarrow a•({\overrightarrow a+\overrightarrow b})$的值等于( )
| A. | 4 | B. | 5 | C. | 6 | D. | $4+\sqrt{3}$ |
6.下列四个结论中不正确的是( )
| A. | 若x>0,则x>sinx恒成立 | |
| B. | 命题“若x-sinx=0,则x=0”的否命题为“若x-sinx≠0,则x≠0” | |
| C. | “命题p∧q为真”是“命题p∨q为真”的充分不必要条件 | |
| D. | 命题“?x∈R,x-lnx>0”的否定是“?x0∈R,x0-lnx0<0” |
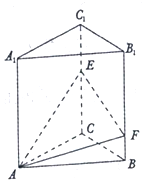 如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1,BB1上的点,且EC=2FB.
如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1,BB1上的点,且EC=2FB.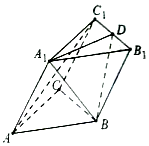 如图,在三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,侧面C1CBB1是矩形.
如图,在三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,侧面C1CBB1是矩形.