题目内容
已知公比大于1的等比数列{an}中,a2=2且6是a1+3与a3+4的等差中项,
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足b1+2b2+3b3+…+nbn=an,求数列{bn}的通项公式.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足b1+2b2+3b3+…+nbn=an,求数列{bn}的通项公式.
考点:数列的求和,等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(I)利用等差数列与等比数列的通项公式即可得出;
(II)利用递推关系即可得出.
(II)利用递推关系即可得出.
解答:
解:(I)公比q大于1的等比数列{an}中,a2=2且6是a1+3与a3+4的等差中项,
∴a1q=2,12=a1+3+a1q2+4,q>1.
解得
,
∴an=2n-1.
(II)∵b1+2b2+3b3+…+nbn=an,
∴当n≥2时,b1+2b2+3b3+…+(n-1)bn-1=an-1,
∴nbn=an-an-1=2n-1-2n-2,
∴bn=
.
当n=1时,b1=a1=1,
∴数列{bn}的通项公式bn=
.
∴a1q=2,12=a1+3+a1q2+4,q>1.
解得
|
∴an=2n-1.
(II)∵b1+2b2+3b3+…+nbn=an,
∴当n≥2时,b1+2b2+3b3+…+(n-1)bn-1=an-1,
∴nbn=an-an-1=2n-1-2n-2,
∴bn=
| 2n-2 |
| n |
当n=1时,b1=a1=1,
∴数列{bn}的通项公式bn=
|
点评:本题考查了等差数列与等比数列的通项公式、递推关系,考查了计算能力,属于基础题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
空间三条直线,任何两条不共面,且两两互相垂直,另一条直线l与这三条直线所成的角均为α,则tanα=( )
| A、1 | ||
B、
| ||
C、
| ||
D、2
|
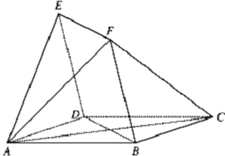 如图,四边形ABCD与BDEF 均为菱形,∠DAB=∠DBF=60°,且FA=FC.
如图,四边形ABCD与BDEF 均为菱形,∠DAB=∠DBF=60°,且FA=FC.