题目内容
函数f(x)的定义域为[0,1],f(0)=f(1),且对任意不同的x1,x2都有|f(x2)-f(x1)|<|x2-x1|,求证:|f(x2)-f(x1)|≤
.
| 1 |
| 2 |
考点:函数单调性的判断与证明
专题:证明题,函数的性质及应用,不等式
分析:根据题意,先证明f(x)在定义域上的极大值和极小值差的绝对值小于
,再证明|f(x2)-f(x1)|小于或等于
.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
证明:∵函数f(x)的定义域为[0,1],对任意不同的x1,x2,
都有|f(x2)-f(x1)|<|x2-x1|成立,
不妨设x=m时,f(m)为最大值;x=n时,f(n)为最小值,(其中0<m<1,0<n<1)
当m<n时,∵|f(x2)-f(x1)|<|x2-x1|,
∴f(m)-f(0)<m①,
f(m)-f(n)<n-m②,
f(1)-f(n)<1-n③,
①+②+③得:2f(m)-2f(n)+f(1)-f(0)<1;
又f(0)=f(1),
∴|f(m)-f(n)|<
;
当n<m时,∵|f(x2)-f(x1)|<|x2-x1|,
∴f(0)-f(n)<n④,
f(m)-f(n)<m-n⑤,
f(m)-f(1)<1-m⑥,
④+⑤+⑥得:2f(m)-2f(n)+f(0)-f(1)<1,
又f(0)=f(1),
∴|f(m)-f(n)|<
;
对于f(0)和f(1)为极大值或极小值时,不妨设x=m时,f(m)为最小值或极大值,
同理可得,|f(m)-f(1)|<
;
∴f(x)的极大值和极小值差的绝对值小于
,
又|f(x2)-f(x1)|小于或等于极大值和极小值差的绝对值;
∴|f(x1)-f(x2)|≤
.
都有|f(x2)-f(x1)|<|x2-x1|成立,
不妨设x=m时,f(m)为最大值;x=n时,f(n)为最小值,(其中0<m<1,0<n<1)
当m<n时,∵|f(x2)-f(x1)|<|x2-x1|,
∴f(m)-f(0)<m①,
f(m)-f(n)<n-m②,
f(1)-f(n)<1-n③,
①+②+③得:2f(m)-2f(n)+f(1)-f(0)<1;
又f(0)=f(1),
∴|f(m)-f(n)|<
| 1 |
| 2 |
当n<m时,∵|f(x2)-f(x1)|<|x2-x1|,
∴f(0)-f(n)<n④,
f(m)-f(n)<m-n⑤,
f(m)-f(1)<1-m⑥,
④+⑤+⑥得:2f(m)-2f(n)+f(0)-f(1)<1,
又f(0)=f(1),
∴|f(m)-f(n)|<
| 1 |
| 2 |
对于f(0)和f(1)为极大值或极小值时,不妨设x=m时,f(m)为最小值或极大值,
同理可得,|f(m)-f(1)|<
| 1 |
| 2 |
∴f(x)的极大值和极小值差的绝对值小于
| 1 |
| 2 |
又|f(x2)-f(x1)|小于或等于极大值和极小值差的绝对值;
∴|f(x1)-f(x2)|≤
| 1 |
| 2 |
点评:本题考查了绝对值不等式|A-B|≤|A|+|B|的应用问题,也考查了分类讨论思想的应用问题,是综合性题目.

练习册系列答案
相关题目
已知命题p:“将函数y=sin(2x+θ)的图象沿x轴向右平移
个单位后,得到一个关于y轴对称的图象”,命题q:“θ=kπ+
(k∈Z)”则p是q的 ( )条件.
| π |
| 16 |
| 5π |
| 8 |
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
已知全集A={0,2,4,6},集合B={2,4,5,6},则A∩B等于( )
| A、{0,2,4,6,} |
| B、{2,4,6} |
| C、{0,2,4,5} |
| D、{0,5} |
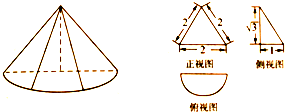 已知图(2)是图(1)所示几何体的三视图,其中俯视图是个半圆,则图(1)所示几何体的表面积为( )
已知图(2)是图(1)所示几何体的三视图,其中俯视图是个半圆,则图(1)所示几何体的表面积为( )A、
| ||||
B、π+
| ||||
C、
| ||||
D、
|
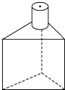
下列选项中不是右图中几何体的三种视图之一的是( )

A、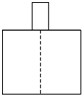 |
B、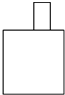 |
C、 |
D、 |
 如图所示,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
如图所示,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BC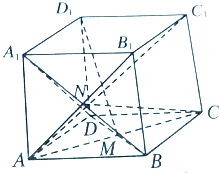 如图,在正方形ABCD-A1B1C1D1中,M,N分别为正方形ABCD和AA1B1B的重心.
如图,在正方形ABCD-A1B1C1D1中,M,N分别为正方形ABCD和AA1B1B的重心.