题目内容
若双曲线
-
=1的离心率为
、则其渐近线的斜率为： ．
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：运用离心率公式可得c=
a，再由a，b，c的关系可得a，b的关系，再由双曲线的渐近线方程，可得斜率．
| 3 |
解答：
解：由双曲线
-
=1的离心率为
，
则e=
=
，
即c=
a，
即有b=
=
a，
则双曲线的渐近线方程为y=±
x，
则渐近线的斜率为±
．
故答案为：±
．
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
则e=
| c |
| a |
| 3 |
即c=
| 3 |
即有b=
| c2-a2 |
| 2 |
则双曲线的渐近线方程为y=±
| b |
| a |
则渐近线的斜率为±
| 2 |
故答案为：±
| 2 |
点评：本题考查双曲线的方程和性质，考查离心率的运用和渐近线方程的运用，考查运算能力，属于基础题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知全集U={1，2，3，4}，集合A={1，2，4}，B={2，3}，则图中阴影部分表示的集合为（ ）| A、{2} |
| B、{3} |
| C、{1，4} |
| D、{1，2，3，4} |
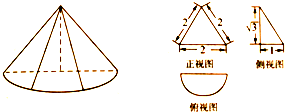已知图（2）是图（1）所示几何体的三视图，其中俯视图是个半圆，则图（1）所示几何体的表面积为（ ）A、
| ||||
B、π+
| ||||
C、
| ||||
D、
|
在空间，下列命题中正确的是 （ ）
| A、没有公共点的两条直线平行 |
| B、与同一直线垂直的两条直线平行 |
| C、平行于同一直线的两条直线平行 |
| D、已知直线a不在平面α内，则直线a∥平面α |
已知直线m，n和平面α，β，若α⊥β，α∩β=m，n?α，要使n⊥β，则应增加的条件是（ ）
| A、m∥n | B、n∥α |
| C、n⊥m | D、n⊥α |
下列函数中，在（-1，1）内有零点且单调递增的是（ ）
A、y=log
| ||
| B、y=-x3 | ||
| C、y=2x-1 | ||
| D、y=x2-2 |