题目内容
已知直线l的参数方程为
,曲线C的参数方程为
,设直线l与曲线C交于两点A,B.
(1)求|AB|;
(2)设P为曲线C上的一点,当△ABP的面积取最大值时,求点P的坐标.
|
|
(1)求|AB|;
(2)设P为曲线C上的一点,当△ABP的面积取最大值时,求点P的坐标.
考点:椭圆的参数方程,直线与圆锥曲线的关系
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)参数方程化为普通方程,再联立求出A,B的坐标,即可求|AB|;
(2)△ABP的面积取最大值时,P到AB的距离最大,利用参数法可求.
(2)△ABP的面积取最大值时,P到AB的距离最大,利用参数法可求.
解答:
解:(1)直线l的参数方程为
可化为x+2y=2,曲线C的参数方程为
,可化为
+y2=1
两方程联立,可得y2-y=0,∴y=0或1,
∴A(2,0),B(0,1),
∴|AB|
;
(2)设P(2cosθ,sinθ),则
P到AB的距离为
=
∴sin(θ+
)=1,即θ=
时d最大,即△ABP的面积取最大值,点P的坐标为(-
,-
).
|
|
| x2 |
| 4 |
两方程联立,可得y2-y=0,∴y=0或1,
∴A(2,0),B(0,1),
∴|AB|
| 5 |
(2)设P(2cosθ,sinθ),则
P到AB的距离为
| |2cosθ+2sinθ-2| | ||
|
|2
| ||||
|
∴sin(θ+
| π |
| 4 |
| 3π |
| 4 |
| 2 |
| ||
| 2 |
点评:本题考查参数方程与普通方程的互化,考查学生的计算能力,比较基础.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
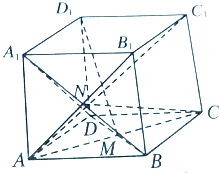 如图,在正方形ABCD-A1B1C1D1中,M,N分别为正方形ABCD和AA1B1B的重心.
如图,在正方形ABCD-A1B1C1D1中,M,N分别为正方形ABCD和AA1B1B的重心. 如图,已知PA⊥矩形ABCD所在的平面,E,F分别为AB,PC的中点,
如图,已知PA⊥矩形ABCD所在的平面,E,F分别为AB,PC的中点,