题目内容
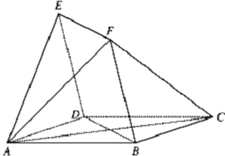 如图,四边形ABCD与BDEF 均为菱形,∠DAB=∠DBF=60°,且FA=FC.
如图,四边形ABCD与BDEF 均为菱形,∠DAB=∠DBF=60°,且FA=FC.(1)求证:FC∥平面EAD;
(2)求证:平面BDEF⊥平面ABCD;
(3)若AB=2,求三棱锥C-AEF的体积.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)由菱形性质得AD∥BC,DE∥BF,从而平面FBC∥平面EAD,由此能证明FC∥平面EAD.
(2)由已知得△DBF为等边三角形,从而FO⊥BD,又FA=FC,从而FO⊥AC,由此能证明平面BDEF⊥平面ABCD.
(3)由EF⊥平面AFC,根据VC-AEF=VE-AFC,利用等积法能求出三棱锥C-AEF的体积.
(2)由已知得△DBF为等边三角形,从而FO⊥BD,又FA=FC,从而FO⊥AC,由此能证明平面BDEF⊥平面ABCD.
(3)由EF⊥平面AFC,根据VC-AEF=VE-AFC,利用等积法能求出三棱锥C-AEF的体积.
解答:
(1)证明:∵四边形ABCD与BDEF均为菱形,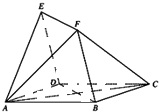
∴AD∥BC,DE∥BF,
∴平面FBC∥平面EAD,
又FC?平面FBC,∴FC∥平面EAD.
(2)解:∵四边形BDEF为菱形,且∠DBF=60°,
∴△DBF为等边三角形,
∵O为BD中点,∴FO⊥BD,又FA=FC,
∴FO⊥AC,故FO⊥平面ABCD,
∴平面BDEF⊥平面ABCD.
(3)解:∵EF⊥平面AFC,
∴点E到平面AFC的距离为2,
∴VC-AEF=VE-AFC=
×
×
×2=2.

∴AD∥BC,DE∥BF,
∴平面FBC∥平面EAD,
又FC?平面FBC,∴FC∥平面EAD.
(2)解:∵四边形BDEF为菱形,且∠DBF=60°,
∴△DBF为等边三角形,
∵O为BD中点,∴FO⊥BD,又FA=FC,
∴FO⊥AC,故FO⊥平面ABCD,
∴平面BDEF⊥平面ABCD.
(3)解:∵EF⊥平面AFC,
∴点E到平面AFC的距离为2,
∴VC-AEF=VE-AFC=
| 1 |
| 3 |
| ||
| 2 |
| 6 |
点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明,考查三棱锥的体积的求法,解题时要注意线面关系、面面关系、菱形、等边三角形性质的合理运用.

练习册系列答案
相关题目
已知全集A={0,2,4,6},集合B={2,4,5,6},则A∩B等于( )
| A、{0,2,4,6,} |
| B、{2,4,6} |
| C、{0,2,4,5} |
| D、{0,5} |
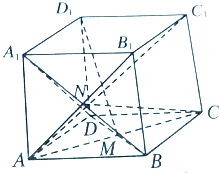 如图,在正方形ABCD-A1B1C1D1中,M,N分别为正方形ABCD和AA1B1B的重心.
如图,在正方形ABCD-A1B1C1D1中,M,N分别为正方形ABCD和AA1B1B的重心.