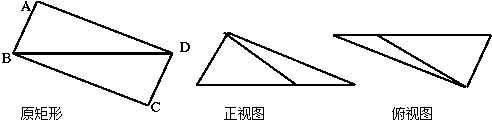
题目内容
空间三条直线，任何两条不共面，且两两互相垂直，另一条直线l与这三条直线所成的角均为α，则tanα=（ ）
| A、1 | ||
B、
| ||
C、
| ||
D、2
|
考点：异面直线及其所成的角,棱锥的结构特征
专题：空间位置关系与距离
分析：在空间取一点O，分别作三条直线的平行线OA，OB，OC，构造一个正方体，则直线l即直线OD所OA、OB、OC所成的角相等均为α，由此利用正方体体的结构特征能求出tanα．
解答：
解：在空间取一点O，
分别作三条直线的平行线OA，OB，OC，
构造一个正方体如右图所示，
则直线l即直线OD与OA、OB、OC所成的角相等均为α，
α=∠COD，设正方体的棱长为1，
则tanα=tan∠COD=
=
．
故选：B．
分别作三条直线的平行线OA，OB，OC，
构造一个正方体如右图所示，
则直线l即直线OD与OA、OB、OC所成的角相等均为α，
α=∠COD，设正方体的棱长为1，
则tanα=tan∠COD=
| CD |
| OC |
| 2 |
故选：B．
点评：本题考查角的正切值的求法，是中档题，解题时要认真审题，注意构造法的合理运用．
练习册系列答案
应用题作业本系列答案
相关题目
如图所示，四边形ABEF和ABCD都是直角梯形，∠BAD=∠FAB=90°，BC已知直线m，n和平面α，β，若α⊥β，α∩β=m，n?α，要使n⊥β，则应增加的条件是（ ）
| A、m∥n | B、n∥α |
| C、n⊥m | D、n⊥α |
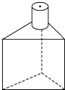
下列选项中不是右图中几何体的三种视图之一的是（ ）
A、 |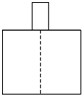
B、 |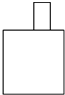
C、 |
D、 |