题目内容
在平面直角坐标系xOy中,已知E:(x+
)2+y2=16,点F(
,0),点P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于点Q.记动点Q的轨迹为C,另有动点M(x,y)(x≥0)到点N(2,0)的距离比它到直线x=-1的距离多1,记点M的轨迹为C1,轨迹C2的方程为x2=y
(1)求轨迹C和C1的方程
(2)已知点T(-1,0),设轨迹C1与C2异于原点O的交点为R,若懂直线l与直线OR垂直,且与轨迹C交于不同的两点A、B,求
•
的最小值
(3)在满足(2)中的条件下,当
•
取得最小值时,求△TAB的面积.
| 3 |
| 3 |
(1)求轨迹C和C1的方程
(2)已知点T(-1,0),设轨迹C1与C2异于原点O的交点为R,若懂直线l与直线OR垂直,且与轨迹C交于不同的两点A、B,求
| TA |
| TB |
(3)在满足(2)中的条件下,当
| TA |
| TB |
考点:轨迹方程,平面向量数量积的运算,直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:(1)根据题意可得|QE|+|QF|=|QE|+|QP|=4>|EF|=2
,由椭圆定义可得点Q的轨迹C的方程为
+y2=1.
直接由抛物线定义可得动点M(x,y)的轨迹C1是以N(2,0)为焦点,以直线x=-2为准线的抛物线,则抛物线轨迹方程可求;
(2)联立两抛物线方程求得R(2,4),写出动直线l的方程,联立直线方程与椭圆方程,化为关于x的一元二次方程后由判别式大于0求得m的范围,利用根与系数的关系得到A,B两点横坐标的和与积,把
•
转化为含m的代数式由二次函数求最值;
(3)把m=-
代入x1+x2=2m,x1x2=2m2-2,得x1+x2=-
,x1x2=-
.由弦长公式求得|AB|,再由点到直线的距离公式求得T到直线l的距离,代入三角形的面积公式得答案.
| 3 |
| x2 |
| 4 |
直接由抛物线定义可得动点M(x,y)的轨迹C1是以N(2,0)为焦点,以直线x=-2为准线的抛物线,则抛物线轨迹方程可求;
(2)联立两抛物线方程求得R(2,4),写出动直线l的方程,联立直线方程与椭圆方程,化为关于x的一元二次方程后由判别式大于0求得m的范围,利用根与系数的关系得到A,B两点横坐标的和与积,把
| TA |
| TB |
(3)把m=-
| 2 |
| 5 |
| 4 |
| 5 |
| 42 |
| 25 |
解答:
 解:(1)如图,
解:(1)如图,
连结QF,根据题意,|QP|=|QF|,则|QE|+|QF|=|QE|+|QP|=4>|EF|=2
,
故动点Q的轨迹C是以E,F为焦点,长轴长为4的椭圆,
设其方程为
+
=1,(a>b>0),可知a=2,c=
,则b=1,
∴点Q的轨迹C的方程为
+y2=1.
∵动点M(x,y)(x≥0)到点N(2,0)的距离比它到直线x=-1的距离多1,
∴动点M(x,y)的轨迹C1是以N(2,0)为焦点,以直线x=-2为准线的抛物线,
∴轨迹方程为y2=8x;
(2)如图,
联立
,解得R(2,4),
∴kOR=2,则可设动直线l的方程为y=-
x+m,
联立
,得x2-2mx+2m2-2=0.
由△=(-2m)2-4(2m2-2)=8-4m2>0,得-
<m<
.
设A(x1,y1),B(x2,y2),
则x1+x2=2m,x1x2=2m2-2.
=(x1+1,y1),
=(x2+1,y2),
∴
•
=(x1+1)(x2+1)+y1y2=x1x2+(x1+x2)+1+(-
x1+m)(-
x2+m)
=
x1x2+(1-
m)(x1+x2)+1+m2=
(2m2-2)+(1-
m)•2m+1+m2
=
(5m2+4m-3)(-
<m<
),
∴当m=-
时,
•
有最小值为-
;
(3)把m=-
代入x1+x2=2m,x1x2=2m2-2.得x1+x2=-
,x1x2=-
.
∴|AB|=
=
.
又T(-1,0)到直线5x+10y+4=0的距离为d=
=
,
∴△TAB的面积S=
×
×
=
.
 解:(1)如图,
解:(1)如图,连结QF,根据题意,|QP|=|QF|,则|QE|+|QF|=|QE|+|QP|=4>|EF|=2
| 3 |
故动点Q的轨迹C是以E,F为焦点,长轴长为4的椭圆,
设其方程为
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
∴点Q的轨迹C的方程为
| x2 |
| 4 |
∵动点M(x,y)(x≥0)到点N(2,0)的距离比它到直线x=-1的距离多1,
∴动点M(x,y)的轨迹C1是以N(2,0)为焦点,以直线x=-2为准线的抛物线,
∴轨迹方程为y2=8x;
(2)如图,

联立
|
∴kOR=2,则可设动直线l的方程为y=-
| 1 |
| 2 |
联立
|
由△=(-2m)2-4(2m2-2)=8-4m2>0,得-
| 2 |
| 2 |
设A(x1,y1),B(x2,y2),
则x1+x2=2m,x1x2=2m2-2.
| TA |
| TB |
∴
| TA |
| TB |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 2 |
| 2 |
∴当m=-
| 2 |
| 5 |
| TA |
| TB |
| 19 |
| 10 |
(3)把m=-
| 2 |
| 5 |
| 4 |
| 5 |
| 42 |
| 25 |
∴|AB|=
1+(-
|
(-
|
| ||
| 5 |
又T(-1,0)到直线5x+10y+4=0的距离为d=
| |-5+4| | ||
|
| ||
| 25 |
∴△TAB的面积S=
| 1 |
| 2 |
| ||
| 5 |
| ||
| 25 |
| ||
| 50 |
点评:本题考查了圆锥曲线方程的求法,考查了直线与圆锥曲线的位置关系,训练了平面向量数量积在解题中的应用,考查了学生的计算能力,是压轴题.

练习册系列答案
相关题目
已知全集A={0,2,4,6},集合B={2,4,5,6},则A∩B等于( )
| A、{0,2,4,6,} |
| B、{2,4,6} |
| C、{0,2,4,5} |
| D、{0,5} |
下列选项中不是右图中几何体的三种视图之一的是( )
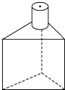

A、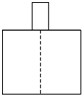 |
B、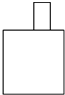 |
C、 |
D、 |

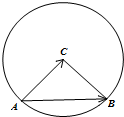 如图,定圆C半径为r,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且
如图,定圆C半径为r,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且