题目内容
已知a>0,且a≠1,设命题p:0<a<1;q:方程ax2-x+
=0有两个不等的实数根.若“p∧q”为假命题,“p∨q”为真命题,求实数a的取值范围.
| 1 |
| 2 |
考点:复合命题的真假
专题:简易逻辑
分析:若命题q为真命题:则a>0,且△>0,解得a的范围.由“p∧q”为假命题,“p∨q”为真命题,可得p与q必然一真一假.解出即可.
解答:
解:若命题q为真命题:则a>0,且△=1-2a>0,解得a<
且a≠0,∴0<a<
.
∵“p∧q”为假命题,“p∨q”为真命题,
∴p与q必然一真一假.
而p假q真是不可能的,因此q假p真,可得
≤a<1.
∴实数a的取值范围是
≤a<1.
| 1 |
| 2 |
| 1 |
| 2 |
∵“p∧q”为假命题,“p∨q”为真命题,
∴p与q必然一真一假.
而p假q真是不可能的,因此q假p真,可得
| 1 |
| 2 |
∴实数a的取值范围是
| 1 |
| 2 |
点评:本题考查了一元二次方程有实数根与判别式的关系、简易逻辑的判定,属于基础题.

练习册系列答案
相关题目
下列选项中不是右图中几何体的三种视图之一的是( )
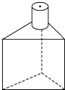

A、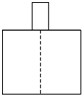 |
B、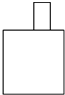 |
C、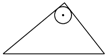 |
D、 |
下列函数中,在(-1,1)内有零点且单调递增的是( )
A、y=log
| ||
| B、y=-x3 | ||
| C、y=2x-1 | ||
| D、y=x2-2 |
点(x,y)的坐标x,y都是有理数时,该点称为有理点,在半径为r,圆心为(a,b)的圆中,若a∈Q,b∈Q,则这个圆上的有理点的数目为( )
| A、最多有一个 |
| B、最多有两个 |
| C、最多有三个 |
| D、可以有无穷多个 |

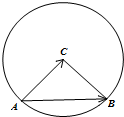 如图,定圆C半径为r,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且
如图,定圆C半径为r,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且