题目内容
已知|
|=6，
与
的夹角为60°，（
+2
）•（
-3
）=-72，则|
|为（ ）
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| A、5 | B、16 | C、5 | D、4 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由条件利用两个向量的数量积的定义可得 2 |
|2+|
|-36=0，由此求得|
|的值．
| b |
| b |
| b |
解答：
解：由题意可得，（
+2
）•（
-3
）=
2-
•
-6
2=36-6|
|•cos60°-6
2=-72，
化简可得 2 |
|2+|
|-36=0，求得|
|=4，
故选：D．
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
| b |
| b |
化简可得 2 |
| b |
| b |
| b |
故选：D．
点评：本题主要考查两个向量的数量积的定义，属于基础题．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
在等比数列{an}中，a4，a12是方程x2+2011x+121=0的两根，则a8的值为（ ）
| A、11 | ||
| B、-11 | ||
| C、±11 | ||
D、
|
如果A为锐角，且cos（π-A）=-
，那么cos（
+A）=（ ）
| 1 |
| 2 |
| π |
| 2 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
“等式lgx=5成立”是“等式lgx2=10成立”的（ ）
| A、充分条件 |
| B、必要条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
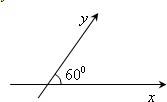如图，在平面斜坐标系xoy中，∠xoy=60°，平面上任一点P在斜坐标系中的斜坐标是这样定义的：若
| OP |
轴方向相同的单位向量），则P点的斜坐标为（x，y）．若P点的斜坐标为（3，-4），则点P到原点O的距离|PO|=（ ）
A、
| ||
B、3
| ||
| C、5 | ||
D、
|
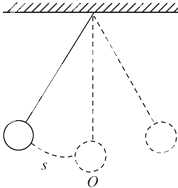如图，单摆从某点开始来回摆动，离开平衡位置O的距离s cm和时间t s的函数关系式为s=6sin（2πt+| π |
| 6 |
| A、2π s |
| B、π s |
| C、0.5 s |
| D、1 s |