题目内容
已知非空集合P满足:①P⊆{1,2,3,4,5},②若a∈P,则(6-a)∈P.符合上述条件的非空集合P有多少个?试写出这些集合来.
考点:元素与集合关系的判断
专题:计算题,集合
分析:由条件列出集合的子集.
解答:
解:∵非空集合P满足:①P⊆{1,2,3,4,5},②若a∈P,则(6-a)∈P.
∴集合P可以有:{1,5},{2,4},{3},{1,5,2,4},{1,5,3},{2,4,3},{1,2,3,4,5}.
共有7个集合.
∴集合P可以有:{1,5},{2,4},{3},{1,5,2,4},{1,5,3},{2,4,3},{1,2,3,4,5}.
共有7个集合.
点评:本题考查了集合的子集的列举方法,属于基础题.

练习册系列答案
相关题目
已知|
|=6,
与
的夹角为60°,(
+2
)•(
-3
)=-72,则|
|为( )
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| A、5 | B、16 | C、5 | D、4 |
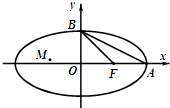 如图,椭圆C:
如图,椭圆C: