题目内容

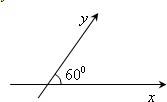如图，在平面斜坐标系xoy中，∠xoy=60°，平面上任一点P在斜坐标系
中的斜坐标是这样定义的：若
OP
=xe1+ye2（其中e1、e2分别为与x轴、y
轴方向相同的单位向量），则P点的斜坐标为（x，y）．若P点的斜坐标为（3，-4），则点P到原点O的距离|PO|=（　　）
A、
13
B、3
3
C、5
D、
11
考点：进行简单的合情推理
专题：平面向量及应用,推理和证明
分析：根据P点的坐标表示出向量
OP
，进而由|
OP
|2=（3
e
1-4
e
2）2可得答案．
解答： 解：∵P点斜坐标为（3，-4），
∴
OP
=3
e
1-4
e
2．
∴|
OP
|2=（3
e
1-4
e
2）2=25-24
e
1•
e
2=25-24×cos60°=13．
∴|
OP
|=
13
，
即|OP|=
13
．
故选：A
点评：本题主要考查平面向量的坐标表示和运算．属中档题．
练习册系列答案
相关题目
如图为某几何体的三视图，则其体积为（　　）
A、2
B、4
C、
4
3
D、
2
3
如图，是某篮球运动员在一个赛季的30场比赛中的得分的茎叶图，则得分的中位数和众数分别为（　　）
A、3和3B、23和3
C、3和23D、23和23
如果二次函数y=x2+2x+（m-2）有两个不同的零点，则m的取值范围是（　　）
A、[3，+∞）
B、（3，+∞）
C、（-∞，3]
D、（-∞，3）
设集合A={-1，1，2}，B={a+1，a2+3}，A∩B={2}，则实数a的值为（　　）
A、1B、2C、3D、0
已知|
a
|=6，
a
与
b
的夹角为60°，（
a
+2
b
）•（
a
-3
b
）=-72，则|
b
|为（　　）
A、5B、16C、5D、4
下列函数中既是奇函数，又在区间（0，+∞）上单调递增的是（　　）
A、y=sinx
B、y=-x2
C、y=xlg2
D、y=-x3
椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别为F1，F2，上顶点为A，在x轴负半轴上有一点B，满足
BF1
=
F1F2
，AB⊥AF2．
（Ⅰ）求椭圆C的离心率．
（Ⅱ）D是过A，B，F2三点的圆上的点，D到直线l：x-
3
y-3=0的最大距离等于椭圆长轴的长，求椭圆C的方程．
设函数f（x）=
3
cos2ωx+sinωxcosωx+a，（ω＞0，a∈R），且f（x）的图象在y轴右侧的第一个最高点的横坐标为
π
6
．
（Ⅰ）求ω的值及对称轴方程：
（Ⅱ）如果f（x）在区间[-
π
3
，
5π
6
]上的最小值为
3
，求a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网