题目内容
已知函数f(x)=2ex-ax-2(a∈R)
(1)讨论函数的单调性;
(2)当x≥0时,f(x)≥0,求a的取值范围.
(1)讨论函数的单调性;
(2)当x≥0时,f(x)≥0,求a的取值范围.
考点:利用导数研究函数的单调性
专题:函数的性质及应用,导数的综合应用
分析:(1)先求函数的定义域,易知x∈R,然后对原函数求导,借助于函数y=2ex的图象,通过变换得到f′(x)=2ex-a的图象,解不等式得到原函数的单调区间.
(2)这是一道不等式恒成立问题,因此只需当x≥0时,f(x)min≥0即可,再结合(1)中对函数单调性的研究,确定f(x)的最小值,则问题可解.
(2)这是一道不等式恒成立问题,因此只需当x≥0时,f(x)min≥0即可,再结合(1)中对函数单调性的研究,确定f(x)的最小值,则问题可解.
解答:
解:(Ⅰ)f′(x)=2ex-a.
若a≤0,则f′(x)>0,f(x)在(-∞,+∞)上单调递增;
若a>0,令f′(x)=0得x=ln
,易知
当x∈(-∞,ln
)时,f′(x)<0,∴f(x)在(-∞,ln
)上单调递减;
当x∈(ln
,+∞)时,f′(x)>0,f(x)在[ln
,+∞)上单调递增;
综上,a≤0时,f(x)在(-∞,+∞)上单调递增;a>0时,f(x)在(-∞,ln
)上单调递减,在ln
,+∞)上单调递增.
(Ⅱ)注意到f(0)=0.
(1)当a≤0时,则当x∈[0,+∞)时,f(x)单调递增,只需f(x)min=f(0)=0,显然成立.
(2)当a>0时
若ln
≤0,即0<a≤2,则当x∈[0,+∞)时,f(x)单调递增,f(x)≥f(0)=0,符合题意.
若ln
>0,即a>2,则当x∈(0,ln
)时,f(x)单调递减,又因为f(0)=0,所以此时f(x)<0,不合题意.
综上所述,a的取值范围是(-∞,2].
若a≤0,则f′(x)>0,f(x)在(-∞,+∞)上单调递增;
若a>0,令f′(x)=0得x=ln
| a |
| 2 |
当x∈(-∞,ln
| a |
| 2 |
| a |
| 2 |
当x∈(ln
| a |
| 2 |
| a |
| 2 |
综上,a≤0时,f(x)在(-∞,+∞)上单调递增;a>0时,f(x)在(-∞,ln
| a |
| 2 |
| a |
| 2 |
(Ⅱ)注意到f(0)=0.
(1)当a≤0时,则当x∈[0,+∞)时,f(x)单调递增,只需f(x)min=f(0)=0,显然成立.
(2)当a>0时
若ln
| a |
| 2 |
若ln
| a |
| 2 |
| a |
| 2 |
综上所述,a的取值范围是(-∞,2].
点评:本题重点考查利用导数研究函数的单调性,以及不等式恒成立问题.对于此类问题在解不等式时要充分利用数形结合的思想辅助分析,进行讨论;而不等式恒成立问题往往转化为函数的最值问题,再进一步利用导数研究函数的单调性求最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将函数y=sin(2x-
)的图象先向左平移
,然后将所得图象上所有点的横坐标变为原来的2倍(纵坐标不变),则所得到的图象对应的函数解析式为( )
| π |
| 3 |
| π |
| 6 |
| A、y=cosx | ||
| B、y=sin4x | ||
C、y=sin(x-
| ||
| D、y=sinx |
已知|
|=6,
与
的夹角为60°,(
+2
)•(
-3
)=-72,则|
|为( )
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| A、5 | B、16 | C、5 | D、4 |
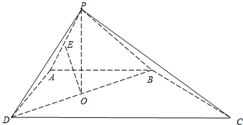 如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点.
如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点. 如图,三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为2的正三角形,且∠BAC=90°,O、D分别为BC、AB的中点.
如图,三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为2的正三角形,且∠BAC=90°,O、D分别为BC、AB的中点.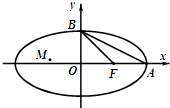 如图,椭圆C:
如图,椭圆C: