题目内容
求关于x的不等式：|x-1|＞|x+1|的解集．
考点：绝对值不等式的解法
专题：计算题,不等式的解法及应用
分析：可将原不等式两边平方，再化简整理，即可得到解集．
解答：
解：|x-1|＞|x+1|?|x-1|2＞|x+1|2
?（x-1）2＞（x+1）2?x2-2x+1＞x2+2x+1?x＜0．
则原不等式的解集为（-∞，0）
?（x-1）2＞（x+1）2?x2-2x+1＞x2+2x+1?x＜0．
则原不等式的解集为（-∞，0）
点评：本题考查绝对值不等式的解法：两边平方法，这是去绝对值的常用方法，属于基础题．
练习册系列答案
相关题目
将函数f（x）=sinωx（其中ω＞0）的图象向左平移
单位长度，所得图象关于x=
对称，则ω的最小值是（ ）
| π |
| 2 |
| π |
| 6 |
| A、6 | ||
B、
| ||
C、
| ||
D、
|
如果二次函数y=x2+2x+（m-2）有两个不同的零点，则m的取值范围是（ ）
| A、[3，+∞） |
| B、（3，+∞） |
| C、（-∞，3] |
| D、（-∞，3） |
已知|
|=6，
与
的夹角为60°，（
+2
）•（
-3
）=-72，则|
|为（ ）
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| A、5 | B、16 | C、5 | D、4 |
下列函数中既是奇函数，又在区间（0，+∞）上单调递增的是（ ）
| A、y=sinx |
| B、y=-x2 |
| C、y=xlg2 |
| D、y=-x3 |
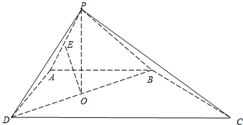如图，四棱锥P-ABCD的底面是直角梯形，AB∥CD，AB⊥AD，△PAB和△PAD是两个边长为2的正三角形，DC=4，O为BD的中点，E为PA的中点．