题目内容
“等式lgx=5成立”是“等式lgx2=10成立”的( )
| A、充分条件 |
| B、必要条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:首先,从两个方面考虑:由“等式lgx=5成立”能否得到“等式lgx2=10成立”;由“等式lgx2=10成立”能否得到“等式lgx=5成立”,然后,结合充分条件和必要条件的判断方法进行求解.
解答:
解:先判断“等式lgx=5成立”能否得到“等式lgx2=10成立”;
∵lgx=5,
∴2lgx=10,
即lgx2=10,
∴等式lgx=5成立”⇒“等式lgx2=10成立”;
再判断“等式lgx2=10成立”能否得到“等式lgx=5成立”,
∵lgx2=10,
当x<0时,显然lgx=5不成立,
∴“等式lgx2=10成立”得不到“等式lgx=5成立”,
∴“等式lgx=5成立”是“等式lgx2=10成立”的充分不必要条件;
故选:A.
∵lgx=5,
∴2lgx=10,
即lgx2=10,
∴等式lgx=5成立”⇒“等式lgx2=10成立”;
再判断“等式lgx2=10成立”能否得到“等式lgx=5成立”,
∵lgx2=10,
当x<0时,显然lgx=5不成立,
∴“等式lgx2=10成立”得不到“等式lgx=5成立”,
∴“等式lgx=5成立”是“等式lgx2=10成立”的充分不必要条件;
故选:A.
点评:本题综合考查了对数的运算性质,充分条件和必要条件等知识,属于中档题.

练习册系列答案
相关题目
下列四个框图中,为结构图的有( )个

| A、1 | B、2 | C、3 | D、4 |
将函数y=sin(2x-
)的图象先向左平移
,然后将所得图象上所有点的横坐标变为原来的2倍(纵坐标不变),则所得到的图象对应的函数解析式为( )
| π |
| 3 |
| π |
| 6 |
| A、y=cosx | ||
| B、y=sin4x | ||
C、y=sin(x-
| ||
| D、y=sinx |
设集合A={x|0<x<2},B={x|y=2sinx},则A∩B=( )
| A、{x|1≤x<2} |
| B、{x|0<x<1} |
| C、{x|0<x≤2} |
| D、{x|0<x<2} |
如果二次函数y=x2+2x+(m-2)有两个不同的零点,则m的取值范围是( )
| A、[3,+∞) |
| B、(3,+∞) |
| C、(-∞,3] |
| D、(-∞,3) |
若向量
=(1,1),
=(1,-1),
=(-2,1),则
等于( )
| a |
| b |
| c |
| c |
A、-
| ||||||||
B、-
| ||||||||
C、-
| ||||||||
D、-
|
已知|
|=6,
与
的夹角为60°,(
+2
)•(
-3
)=-72,则|
|为( )
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| A、5 | B、16 | C、5 | D、4 |
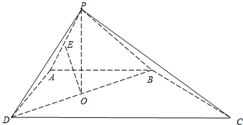 如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点.
如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点.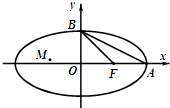 如图,椭圆C:
如图,椭圆C: