题目内容
已知关于x的方程x2+3x+2a-3=0在（1，3]上有解，则实数a的取值范围为 ．
考点：函数的零点与方程根的关系
专题：计算题,函数的性质及应用
分析：方程x2+3x+2a-3=0可化为2a=-（x2+3x）+3；从而可得-15≤2a＜-1；从而解得．
解答：
解：方程x2+3x+2a-3=0可化为
2a=-（x2+3x）+3；
∵1＜x≤3；
∴4＜x2+3x≤18，
故-15≤-（x2+3x）+3＜-1；
即-15≤2a＜-1；
则实数a的取值范围为：[-
，-
）；
故答案为：[-
，-
）．
2a=-（x2+3x）+3；
∵1＜x≤3；
∴4＜x2+3x≤18，
故-15≤-（x2+3x）+3＜-1；
即-15≤2a＜-1；
则实数a的取值范围为：[-
| 15 |
| 2 |
| 1 |
| 2 |
故答案为：[-
| 15 |
| 2 |
| 1 |
| 2 |
点评：本题考查了方程的解与函数的值域的关系应用，属于基础题．
练习册系列答案
课时训练江苏人民出版社系列答案
相关题目
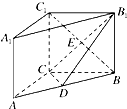如图，在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5，点D是线段AB上的一点，且∠CDB1=90°，AA1=CD，则点A1到平面B1CD的距离为
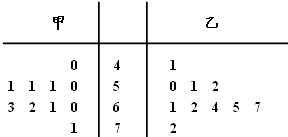随机抽取某中学甲、乙两班各10名学生，测量他们的体重（单位：kg），获得体重数据的茎叶图如图：
已知三个函数f（x）=2+x，g（x）=x-2，h（x）=log2x+x的零点依次为a，b，c，则（ ）
| A、a＜b＜c |
| B、a＜c＜b |
| C、b＜a＜c |
| D、c＜a＜b |