题目内容
某玩具厂所需成本为P元,且P与生产套数x的关系为P=1000+5x+
x2,而每套售出的价格为Q元,其中Q(x)=a+
(a,b∈R).
(1)该玩具厂生产多少套玩具时每套所需成本最少?
(2)若生产出的玩具能全部售出,且当产量为150套时利润最大,此时每套价格为30元,求常数a,b的值.(利润=销售收入-成本)
| 1 |
| 10 |
| x |
| b |
(1)该玩具厂生产多少套玩具时每套所需成本最少?
(2)若生产出的玩具能全部售出,且当产量为150套时利润最大,此时每套价格为30元,求常数a,b的值.(利润=销售收入-成本)
考点:函数模型的选择与应用
专题:函数的性质及应用
分析:(1)建立函数的解析式,再利用基本不等式求函数的最值;
(2)根据利润=销售收入-成本,求出利润函数,再利用当产量为150套时利润最大,此时每套价格为30元,结合二次函数的性质建立条件关系,即可求a,b的值
(2)根据利润=销售收入-成本,求出利润函数,再利用当产量为150套时利润最大,此时每套价格为30元,结合二次函数的性质建立条件关系,即可求a,b的值
解答:
解:(1)由题意,每套玩具所需成本费用为
=
=
+
+5≥2
+5=2
+5=25,
当且仅当
=
,
即x=100时,每套玩具所需成本费用最少为25元.
(2)利润y=xQ(x)-P=x(a+
)-(1000+5x+
x2)=(
-
)x2+(a-5)x-1000,
∵若生产出的玩具能全部售出,且当产量为150套时利润最大,此时每套价格为30元,
∴满足
,
解得a=25,b=30.
| P |
| x |
1000+5x+
| ||
| x |
| x |
| 10 |
| 1000 |
| x |
|
| 100 |
当且仅当
| x |
| 10 |
| 1000 |
| x |
即x=100时,每套玩具所需成本费用最少为25元.
(2)利润y=xQ(x)-P=x(a+
| x |
| b |
| 1 |
| 10 |
| 1 |
| b |
| 1 |
| 10 |
∵若生产出的玩具能全部售出,且当产量为150套时利润最大,此时每套价格为30元,
∴满足
|
解得a=25,b=30.
点评:本题考查函数模型的构建,考查利用基本不等式求函数的最值,考查二次函数的最值,确立函数模型是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
执行如图所示的程序框图,若输出的s的值是100,则框图中的n的值是( )


| A、3 | B、4 | C、5 | D、6 |
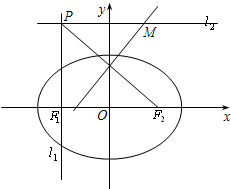 椭圆G:
椭圆G: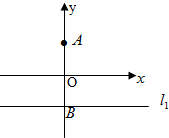 已知定点A(0,a)(a>0),直线l1:y=-a交y轴于点B,记过点A且与直线l1相切的圆的圆心为点C.
已知定点A(0,a)(a>0),直线l1:y=-a交y轴于点B,记过点A且与直线l1相切的圆的圆心为点C.