题目内容
如表是某校高一年级一次考试中数学和英语的成绩抽样:
若抽取学生n人,成绩分为A(优秀)、B(良好)、C(及格)三个等级,设x,y分别表示数学成绩与英语成绩.例如:表中数学成绩为B等级的共有20+18+4=42人,已知x与y均为B等级的概率是0.18.
(1)若在该样本中,数学成绩优秀是30%,求a,b的值;
(2)在英语成绩为C等级的学生中,已知a=10,b=8,求数学成绩为A等级的人数比C等级的人数少数少的概率.
 | A | B | C |
| A | 7 | 20 | 5 |
| B | 9 | 18 | 6 |
| C | a | 4 | b |
(1)若在该样本中,数学成绩优秀是30%,求a,b的值;
(2)在英语成绩为C等级的学生中,已知a=10,b=8,求数学成绩为A等级的人数比C等级的人数少数少的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)由由
=0.3,得a=14,由此能求出b的值.
(2)由题意,知a+b=31,且a≥10,b≥8,用列举法满足条件的(a,b)有14组,且每组出现的可能性相同,找出其中数学成绩为A等级的人数比C等级的人数少的有6组,根据概率公式计算即可.
| 7+9+a |
| 100 |
(2)由题意,知a+b=31,且a≥10,b≥8,用列举法满足条件的(a,b)有14组,且每组出现的可能性相同,找出其中数学成绩为A等级的人数比C等级的人数少的有6组,根据概率公式计算即可.
解答:
解:(1)由
=0,3,得a=14,
∵7+9+a+20+18+4+5+6+b=100,
解得b=17.
(2)由题意,知a+b=31,且a≥10,b≥8,
∴满足条件的(a,b)有:(10,21),(11,20),
(12,19),(13,18),(14,17),(15,16),(16,15),
(17,14),(18,13),(19,12),(20,11),
(21,10),(22,9),(23,8)共14组,
且每组出现的可能性相同.
其中数学成绩为A等级的人数比C等级的人数少:
(10,21),(11,21),(12,19),(13,18),(14,17),(15,16)共6组.
∴数学成绩为A等级的人数比C等级的人数少数少概率为
=
.
| 7+9+a |
| 100 |
∵7+9+a+20+18+4+5+6+b=100,
解得b=17.
(2)由题意,知a+b=31,且a≥10,b≥8,
∴满足条件的(a,b)有:(10,21),(11,20),
(12,19),(13,18),(14,17),(15,16),(16,15),
(17,14),(18,13),(19,12),(20,11),
(21,10),(22,9),(23,8)共14组,
且每组出现的可能性相同.
其中数学成绩为A等级的人数比C等级的人数少:
(10,21),(11,21),(12,19),(13,18),(14,17),(15,16)共6组.
∴数学成绩为A等级的人数比C等级的人数少数少概率为
| 6 |
| 14 |
| 3 |
| 7 |
点评:本题考查概率的求法,解题时要认真审题,注意列举法的合理运用.属于基础题.

练习册系列答案
相关题目
已知正三棱锥的底面边长为
,各侧面均为直角三角形,则它的外接球体积为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
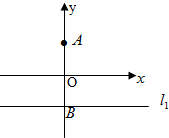 已知定点A(0,a)(a>0),直线l1:y=-a交y轴于点B,记过点A且与直线l1相切的圆的圆心为点C.
已知定点A(0,a)(a>0),直线l1:y=-a交y轴于点B,记过点A且与直线l1相切的圆的圆心为点C. 已知F1、F2为为双曲线C:
已知F1、F2为为双曲线C: