题目内容
设函数f(x)=sin2x+cos(2x+
)
(Ⅰ)求函数f(x)的最大值及此时x的取值集合;
(Ⅱ)设A,B,C为△ABC的三个内角,若cosB=
,f(
)=-
,且C为锐角,求sinA的值.
| π |
| 3 |
(Ⅰ)求函数f(x)的最大值及此时x的取值集合;
(Ⅱ)设A,B,C为△ABC的三个内角,若cosB=
| 1 |
| 3 |
| C |
| 2 |
| 1 |
| 4 |
考点:三角函数中的恒等变换应用,正弦定理
专题:计算题,三角函数的求值
分析:(Ⅰ)利用三角恒等变换公式化简f(x)=
+
cos2x-
sin2x=
-
sin2x,从而求最大值及最大值点;
(Ⅱ)由f(
)=
-
sinC=-
可得sinC=
,从而得到C=
,则sinA=sin(
-B)=
cosB+
sinB,从而求值.
| 1-cos2x |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
(Ⅱ)由f(
| C |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| ||
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
解答:
解:(Ⅰ)f(x)=
+
cos2x-
sin2x=
-
sin2x,…(2分)
∴当sin2x=-1时,
f(x)max=
; …(4分)
此时2x=2kπ-
(k∈Z),
∴x的取值集合为{x|x=kπ-
,k∈Z}. …(6分)
(Ⅱ)∵f(
)=
-
sinC=-
,
∴sinC=
,
∵C为锐角,
∴C=
,…(8分)
由cosB=
得sinB=
=
,
∴sinA=sin(
-B)=
cosB+
sinB=
. …(12分)
| 1-cos2x |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴当sin2x=-1时,
f(x)max=
1+
| ||
| 2 |
此时2x=2kπ-
| π |
| 2 |
∴x的取值集合为{x|x=kπ-
| π |
| 4 |
(Ⅱ)∵f(
| C |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
∴sinC=
| ||
| 2 |
∵C为锐角,
∴C=
| π |
| 3 |
由cosB=
| 1 |
| 3 |
| 1-cos2B |
2
| ||
| 3 |
∴sinA=sin(
| 2π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||||
| 6 |
点评:本题考查了三角恒变换及三角函数的性质应用,属于基础题.

练习册系列答案
相关题目
对于一个容量为N的总体抽取容量为n的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同的方法抽取样本时,总体中每个个体被抽中的概率分别为P1,P2,P3,则( )
| A、P1=P2=P3 |
| B、P1=P2<P3 |
| C、P2=P3<P1 |
| D、P1=P3<P2 |
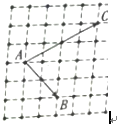 如图所示的方格纸上有三个点A,B,C,且每个小方格的边长为1.
如图所示的方格纸上有三个点A,B,C,且每个小方格的边长为1.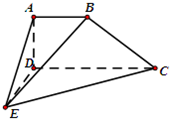 如图,在四棱锥E-ABCD中,AB∥CD,CD=2AB,
如图,在四棱锥E-ABCD中,AB∥CD,CD=2AB,