题目内容
已知圆O的方程为x2+y2=25,设点P(x1,y1),直线m:x1x+y1y=25.
(1)若点P在圆O内,试判断直线m与圆O的位置关系;
(2)若点P在圆O上,且x1=3,y1>0,过点P作直线PA,PB分别交圆O于两点A,B,且直线PA,PB的斜率互为相反数.
①若直线PA过点O,求tan∠APB的值;
②试问:不论直线PA的斜率怎样变化,直线AB的斜率是否总为定值?若是,求出该定值;若不是,请说明理由.
(1)若点P在圆O内,试判断直线m与圆O的位置关系;
(2)若点P在圆O上,且x1=3,y1>0,过点P作直线PA,PB分别交圆O于两点A,B,且直线PA,PB的斜率互为相反数.
①若直线PA过点O,求tan∠APB的值;
②试问:不论直线PA的斜率怎样变化,直线AB的斜率是否总为定值?若是,求出该定值;若不是,请说明理由.
考点:直线与圆的位置关系,直线的斜率
专题:综合题,直线与圆
分析:(1)由点P在圆O内,求得圆心到直线的距离d大于半径,可得直线和圆相离.
(2)①由条件求得点P(3,4),若直线PA过点O,求得PA的斜率,可得PB的斜率,再利用两条直线的夹角公式求得tan∠APB的值;
②求出A,B的坐标,利用斜率公式,即可得出结论.
(2)①由条件求得点P(3,4),若直线PA过点O,求得PA的斜率,可得PB的斜率,再利用两条直线的夹角公式求得tan∠APB的值;
②求出A,B的坐标,利用斜率公式,即可得出结论.
解答:
解:(1)∵点P在圆O内,∴圆心到直线l的距离d=
>5,
∴直线l与圆O相离;
(2)①点P在圆O上,且x1=3,y1>0,得y1=5,即P(3,4).
由题意,AP是圆的直径,所以点P的坐标为(-3,-4),且kAP=
.
又直线PA,PB的斜率互为相反数,所以kPB=-
∴tan∠APB=-
;
②记直线PA的斜率为k,则直线PA的方程为:y=kx+4-3k.
将y=kx+4-3k代入圆O的方程得:x2+(kx+4-3k)2=25,
化简得:(k2+1)x2+2k(4-3k)x+(4-3k)2-25=0,
∵3是方程的一个根,∴3xA=
,∴xA=
由题意知:kPB=-k,同理可得,xB=
∴kAB=k•
=
即kAB=
.
| 25 | ||
|
∴直线l与圆O相离;
(2)①点P在圆O上,且x1=3,y1>0,得y1=5,即P(3,4).
由题意,AP是圆的直径,所以点P的坐标为(-3,-4),且kAP=
| 4 |
| 3 |
又直线PA,PB的斜率互为相反数,所以kPB=-
| 4 |
| 3 |
∴tan∠APB=-
| 24 |
| 7 |
②记直线PA的斜率为k,则直线PA的方程为:y=kx+4-3k.
将y=kx+4-3k代入圆O的方程得:x2+(kx+4-3k)2=25,
化简得:(k2+1)x2+2k(4-3k)x+(4-3k)2-25=0,
∵3是方程的一个根,∴3xA=
| (4-3k)2-25 |
| k2+1 |
| 3k2-8k-3 |
| k2+1 |
由题意知:kPB=-k,同理可得,xB=
| 3k2+8k-3 |
| 1-k2 |
∴kAB=k•
| xA+xB-6 |
| xA-xB |
| 3 |
| 4 |
即kAB=
| 3 |
| 4 |
点评:本题主要考查点和圆的位置关系,直线和圆的位置关系,直线的倾斜角和斜率,两条直线的夹角公式的应用,属于中档题.

练习册系列答案
相关题目
函数f(x)=log2(x+1)-
的零点的个数是( )
| 2 |
| x |
| A、0 | B、1 | C、2 | D、3 |
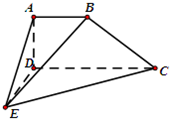 如图,在四棱锥E-ABCD中,AB∥CD,CD=2AB,
如图,在四棱锥E-ABCD中,AB∥CD,CD=2AB,