题目内容
已知函数f(x)=(x2+ax)ex在(0,1)上单调递减.
(Ⅰ)求a的取值范围;
(Ⅱ)令g(x)=[(a+3)x+a2+2a-1]ex,h(x)=f′(x)-g(x),求h(x)在[1,2]上的最小值.
(Ⅰ)求a的取值范围;
(Ⅱ)令g(x)=[(a+3)x+a2+2a-1]ex,h(x)=f′(x)-g(x),求h(x)在[1,2]上的最小值.
考点:利用导数求闭区间上函数的最值
专题:综合题,分类讨论,导数的综合应用
分析:(Ⅰ)求导得f′(x)=(x2+ax+2x+a)ex,f(x)在(0,1)上单调递减,等价于f′(x)≤0在(0,1)上恒成立.只需M(x)=x2+ax+2x+a≤0在(0,1)上恒成立.由二次函数的性质可得不等式组,解出即可;
(Ⅱ)可求h(x)=(x2-x-a2-a+1)ex,h′(x)=(x+a+1)(x-a)ex,可知a∉[1,2],-a-1∈[
,+∞).按照极值点-a-1在区间(1,2)左侧、区间内、区间右侧三种情况进行讨论,由单调性可求得函数的最小值;
(Ⅱ)可求h(x)=(x2-x-a2-a+1)ex,h′(x)=(x+a+1)(x-a)ex,可知a∉[1,2],-a-1∈[
| 1 |
| 2 |
解答:
解:(Ⅰ)f′(x)=(2x+a)ex+(x2+ax)ex=(x2+ax+2x+a)ex,
若f(x)在(0,1)上单调递减,
则f′(x)≤0在(0,1)上恒成立.
而ex>0,只需M(x)=x2+ax+2x+a≤0在(0,1)上恒成立.
于是
,
解得a≤-
.
(Ⅱ)h(x)=f′(x)-g(x)=(x2-x-a2-a+1)ex,
则h′(x)=(x2+x-a2-a)ex=(x+a+1)(x-a)ex,
令h′(x)=0,得x1=a,x2=-a-1,
∵a≤-
,∴a∉[1,2],-a-1∈[
,+∞).
①若-a-1∈[
,1],即a∈[-2,-
]时,h′(x)>0在[1,2]上成立,
此时h(x)在[1,2]上单调递增,
∴h(x)有最小值h(1)=(-a2-a+1)e;
②若-a-1∈(1,2)即a∈(-3,-2)时,当x∈(1,-a-1)时有h′(x)<0,
此时h(x)在(1,-a-1)上单调递减,
当x∈(-a-1,2)时有h′(x)>0,此时h(x)在(-a-1,2)上单调递增,
∴h(x)有最小值h(-a-1)=(2a+3)e-a-1;
③若-a-1∈[2,+∞)即a∈(-∞,-3]时,h′(x)<0在[1,2]上成立,
此时h(x)在[1,2]上单调递减,
h(x)有最小值h(2)=(-a2-a+3)ex.
若f(x)在(0,1)上单调递减,
则f′(x)≤0在(0,1)上恒成立.
而ex>0,只需M(x)=x2+ax+2x+a≤0在(0,1)上恒成立.
于是
|
解得a≤-
| 3 |
| 2 |
(Ⅱ)h(x)=f′(x)-g(x)=(x2-x-a2-a+1)ex,
则h′(x)=(x2+x-a2-a)ex=(x+a+1)(x-a)ex,
令h′(x)=0,得x1=a,x2=-a-1,
∵a≤-
| 3 |
| 2 |
| 1 |
| 2 |
①若-a-1∈[
| 1 |
| 2 |
| 3 |
| 2 |
此时h(x)在[1,2]上单调递增,
∴h(x)有最小值h(1)=(-a2-a+1)e;
②若-a-1∈(1,2)即a∈(-3,-2)时,当x∈(1,-a-1)时有h′(x)<0,
此时h(x)在(1,-a-1)上单调递减,
当x∈(-a-1,2)时有h′(x)>0,此时h(x)在(-a-1,2)上单调递增,
∴h(x)有最小值h(-a-1)=(2a+3)e-a-1;
③若-a-1∈[2,+∞)即a∈(-∞,-3]时,h′(x)<0在[1,2]上成立,
此时h(x)在[1,2]上单调递减,
h(x)有最小值h(2)=(-a2-a+3)ex.
点评:该题考查利用导数研究函数的单调性、最值,考查分类讨论思想,根据极值点与区间的位置关系分类讨论是解决(Ⅱ)问的关键.

练习册系列答案
相关题目
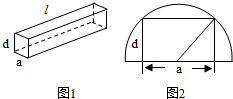 如图1所示,一根水平放置的长方体枕木的安全负荷与它的宽度a成正比,与它的厚度d的平方成正比,与它的长度l的平方成反比.
如图1所示,一根水平放置的长方体枕木的安全负荷与它的宽度a成正比,与它的厚度d的平方成正比,与它的长度l的平方成反比.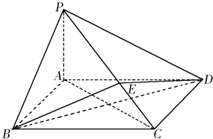 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.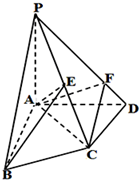 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC=3
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC=3