题目内容
在△ABC中，角A，B，C的对边分别为a，b，c，（2a-c）cosB=bcosC
（Ⅰ）求角B的大小；
（Ⅱ）若b=
，求a+c的最大值．
（Ⅰ）求角B的大小；
（Ⅱ）若b=
| 3 |
考点：余弦定理,正弦定理
专题：解三角形
分析：（Ⅰ）已知等式利用正弦定理化简，整理后利用两角和与差的正弦函数公式及诱导公式化简，根据sinA不为0求出cosB的值，即可确定出B的大小；
（Ⅱ）利用余弦定理列出关系式，将b与cosB的值代入，利用完全平方公式变形，再利用基本不等式即可求出a+c的最大值．
（Ⅱ）利用余弦定理列出关系式，将b与cosB的值代入，利用完全平方公式变形，再利用基本不等式即可求出a+c的最大值．
解答：
解：（Ⅰ）将（2a-c）cosB=bcosC，利用正弦定理化简得：（2sinA-sinC）cosB=sinBcosC，
整理得：2sinAcosB=sinBcosC+sinCcosB=sin（B+C）=sinA，
∵sinA≠0，
∴cosB=
，
则B=
；
（Ⅱ）∵b=
，cosB=
，
∴由余弦定理得：b2=a2+c2-2accosB，即3=a2+c2-ac=（a+c）2-3ac，
∵（a+c）2-3ac≥（a+c）2-3×（
）2=
，
∴3≥
，
则a+c≤2
，当且仅当a=c=
时，a+c取得最大值为2
．
整理得：2sinAcosB=sinBcosC+sinCcosB=sin（B+C）=sinA，
∵sinA≠0，
∴cosB=
| 1 |
| 2 |
则B=
| π |
| 3 |
（Ⅱ）∵b=
| 3 |
| 1 |
| 2 |
∴由余弦定理得：b2=a2+c2-2accosB，即3=a2+c2-ac=（a+c）2-3ac，
∵（a+c）2-3ac≥（a+c）2-3×（
| a+c |
| 2 |
| (a+c)2 |
| 4 |
∴3≥
| (a+c)2 |
| 4 |
则a+c≤2
| 3 |
| 3 |
| 3 |
点评：此题考查了正弦、余弦定理，基本不等式的应用，熟练掌握定理是解本题的关键．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
定义区间（a，b）、[a，b）、（a，b]、[a，b]的长度d均为d=b-a，多个互无交集的区间的并集长度为各区间长度之和，例如（1，2）∪[3，5）的长度d=（2-1）+（5-3）=3．用[x]表示不超过x的最大整数，例如[2]=2，[3.7]=3，[-1.2]=-2．记{x}=x-[x]，设f（x）=[x]•{x}，g（x）=x-1，若用d1、d2和d3分别表示不等式f（x）＞g（x）、方程f（x）=g（x）和不等式f（x）＜g（x）解集区间的长度，则当0≤x≤2013时，有（ ）
| A、d1=1，d2=2，d3=2010 |
| B、d1=1，d2=1，d3=2011 |
| C、d1=3，d2=5，d3=2005 |
| D、d1=2，d2=3，d3=2008 |
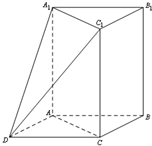如图，三棱柱ABC-A1B1C1中，AA1⊥平面ABC，∠ACB=90°，AC=BC=1，AA1=2．以AB，BC为邻边作平行四边形ABCD，连接DA1和DC1．