题目内容
为了降低能源损耗,三明市某室内体育馆的外墙需要建造隔热层,体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=
(0≤x≤10),已知隔热层厚度为1cm时,每年能源消耗费用为5万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(Ⅰ)求k的值及f(x)的表达式.
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
| 40 |
| kx+5 |
(Ⅰ)求k的值及f(x)的表达式.
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(Ⅰ)由每年的能源消耗费用为C(x),当x=1时,可得k的值;又加装隔热层的费用为C1(x),所以总费用函数f(x)可表示出来,其定义域可得;
(Ⅱ)对函数f(x)变形,利用基本不等式求得最值,即得所求.
(Ⅱ)对函数f(x)变形,利用基本不等式求得最值,即得所求.
解答:
解:(Ⅰ)x=1时,c=5,∴k=3,
∴C(x)=
,
∴f(x)=6z+
=6x+
(0≤x≤10);
(Ⅱ)设3x+5=t,t∈[5,35],则y=2t+
-10≥2
-10=70,
当且仅当2t=
,即t=20时等号成立,此时x=5,f(x)的最小值为70,
∴当隔热层修建5cm厚时,总费用达到最小值为70万元.
∴C(x)=
| 40 |
| 3x+5 |
∴f(x)=6z+
| 20×40 |
| 3x+5 |
| 800 |
| 3x+5 |
(Ⅱ)设3x+5=t,t∈[5,35],则y=2t+
| 800 |
| t |
2t•
|
当且仅当2t=
| 800 |
| t |
∴当隔热层修建5cm厚时,总费用达到最小值为70万元.
点评:本题考查了平均值不等式在函数极值中的应用,在利用平均值不等式求最值时,要注意等号成立的条件是什么.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知△ABC中,|
|=10,
•
=-16,D为边BC的中点,则|
|等于( )
| BC |
| AB |
| AC |
| AD |
| A、6 | B、5 | C、4 | D、3 |
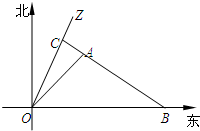 如图所示,一科学考察船从港口O出发,沿北偏东α角的射线OZ方向航行,而在离港口3
如图所示,一科学考察船从港口O出发,沿北偏东α角的射线OZ方向航行,而在离港口3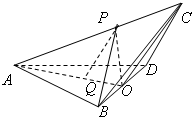 如图,三棱锥C-ABD中,AB=AD=BD=BC=CD=2,O为BD的中点,∠AOC=120°,P为AC上一点,Q为AO上一点,且
如图,三棱锥C-ABD中,AB=AD=BD=BC=CD=2,O为BD的中点,∠AOC=120°,P为AC上一点,Q为AO上一点,且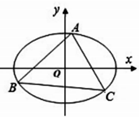 已知椭圆C:
已知椭圆C: