题目内容
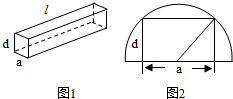如图1所示，一根水平放置的长方体枕木的安全负荷与它的宽度a成正比，与它的厚度d的平方成正比，与它的长度l的平方成反比．（1）若a＞d，将此枕木翻转90°（即宽度变为了厚度），枕木的安全负荷会变大吗？为什么？
（2）现有一根横截面为半圆，半径为
| 3 |
考点：不等式的综合,弧度与角度的互化
专题：不等式
分析：（1）根据题意，可设原来的安全负荷为y1=k•
，k为正常数，由翻转90°后，安全负荷为y2=k•
，然后通过作商比较大小，讨论a、d的大小关系，可得正确结论；
（2）半圆的半径为R，设截取的枕木宽为a，高为d，则根据垂径定理，得a2+4d2=4R2．根据木材长度l为枕木规定的长度是一个不变的定值，得到当u=ad2最大时，安全负荷最大，建立关系式u=d2
．利用基本不等式可得d=
，a=2时，安全负荷最大．
| ad2 |
| l2 |
| da2 |
| l2 |
（2）半圆的半径为R，设截取的枕木宽为a，高为d，则根据垂径定理，得a2+4d2=4R2．根据木材长度l为枕木规定的长度是一个不变的定值，得到当u=ad2最大时，安全负荷最大，建立关系式u=d2
| a2 |
| 2 |
解答：
解：（1）由题意设安全负荷为y1=k•
，k为正常数，
由翻转90°后，安全负荷为y2=k•
，
∵
=
，0＜d＜a，
∴y1＜y2，
∴枕木的安全负荷会变大．
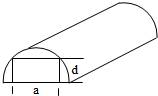
（2）如图，设截取有枕木宽度为a，高为d，
根据垂径定理，得(
)2+d2=R2，即a2+4d2=4R2，
∵∵枕木长度不变，
∴u=ad2最大时，安全负荷最大
∴u=d2
=d 2
=2
=4
≤4
=4，
当且仅当
=3-d2，即d=
，a=2时，u最大，即安全负荷最大．
解：（1）由题意设安全负荷为y1=k•| ad2 |
| l2 |
由翻转90°后，安全负荷为y2=k•
| da2 |
| l2 |
∵
| y1 |
| y2 |
| d |
| a |
∴y1＜y2，
∴枕木的安全负荷会变大．
（2）如图，设截取有枕木宽度为a，高为d，
根据垂径定理，得(
| a |
| 2 |
∵∵枕木长度不变，
∴u=ad2最大时，安全负荷最大
∴u=d2
| a2 |
| 12-4d2 |
| d4(3-d2) |
=4
|
≤4
|
=4，
当且仅当
| d2 |
| 2 |
| 2 |
点评：本题借助于一个实际问题，通过求枕木安全负荷的最值，着重考查了基本不等式在最值问题中的应用，考查了根据实际问题选择函数类型的方法，属于中档题
练习册系列答案
相关题目
n∈N*，则（20-n）（21-n）…（100-n）等于（ ）
A、A
| ||
B、A
| ||
C、A
| ||
D、A
|
抛物线的顶点在原点，对称轴是x轴，抛物线上点（-5，m）到焦点距离是6，则抛物线的标准方程是（ ）
| A、y2=-2x |
| B、y2=-4x |
| C、y2=2x |
| D、y2=-4x或y2=-36x |
定义区间（a，b）、[a，b）、（a，b]、[a，b]的长度d均为d=b-a，多个互无交集的区间的并集长度为各区间长度之和，例如（1，2）∪[3，5）的长度d=（2-1）+（5-3）=3．用[x]表示不超过x的最大整数，例如[2]=2，[3.7]=3，[-1.2]=-2．记{x}=x-[x]，设f（x）=[x]•{x}，g（x）=x-1，若用d1、d2和d3分别表示不等式f（x）＞g（x）、方程f（x）=g（x）和不等式f（x）＜g（x）解集区间的长度，则当0≤x≤2013时，有（ ）
| A、d1=1，d2=2，d3=2010 |
| B、d1=1，d2=1，d3=2011 |
| C、d1=3，d2=5，d3=2005 |
| D、d1=2，d2=3，d3=2008 |
已知△ABC中，|
|=10，
•
=-16，D为边BC的中点，则|
|等于（ ）
| BC |
| AB |
| AC |
| AD |
| A、6 | B、5 | C、4 | D、3 |
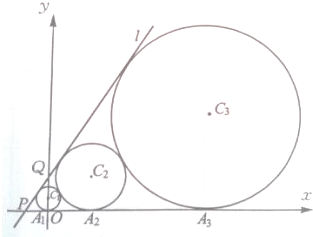如图，在平面直角坐标系中，直线l经过点P（-1，0），Q（0，