题目内容
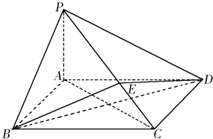 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.(Ⅰ)证明:BD⊥平面PAC;
(Ⅱ)若PA=1,AD=2,求三棱锥E-BCD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)先由线面垂直的性质证出PA⊥BD与PC⊥BD,再由线面垂直的判定定理证明线面垂直即可;
(Ⅱ)设AC与BD的交点为O,连结OE,利用VE-BCD=
S△CEO•BD,可求三棱锥E-BCD的体积.
(Ⅱ)设AC与BD的交点为O,连结OE,利用VE-BCD=
| 1 |
| 3 |
解答:
(Ⅰ)证明:∵PA⊥平面ABCD,BD?面ABCD,
∴PA⊥BD.
∵PC⊥平面BDE,BD?平面BDE,
∴PC⊥BD.
又PA∩PC=P,∴BD⊥平面PAC.…(6分)
(Ⅱ)解:如图,设AC与BD的交点为O,连结OE.
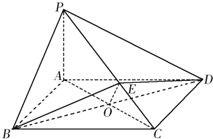
∵PC⊥平面BDE,∴PC⊥OE.
由(Ⅰ)知,BD⊥平面PAC,∴BD⊥AC,
由题设条件知,四边形ABCD为正方形.
由AD=2,得AC=BD=2
,OC=
.
在Rt△PAC中,PC=
=
=3.
易知Rt△PAC∽Rt△OEC,
∴
=
=
,即
=
=
,∴OE=
,CE=
.
∴VE-BCD=
S△CEO•BD=
•
OE•CE•BD=
•
•
•2
=
.…(13分)
∴PA⊥BD.
∵PC⊥平面BDE,BD?平面BDE,
∴PC⊥BD.
又PA∩PC=P,∴BD⊥平面PAC.…(6分)
(Ⅱ)解:如图,设AC与BD的交点为O,连结OE.

∵PC⊥平面BDE,∴PC⊥OE.
由(Ⅰ)知,BD⊥平面PAC,∴BD⊥AC,
由题设条件知,四边形ABCD为正方形.
由AD=2,得AC=BD=2
| 2 |
| 2 |
在Rt△PAC中,PC=
| PA2+AC2 |
12+(2
|
易知Rt△PAC∽Rt△OEC,
∴
| OE |
| PA |
| CE |
| AC |
| OC |
| PC |
| OE |
| 1 |
| CE | ||
2
|
| ||
| 3 |
| ||
| 3 |
| 4 |
| 3 |
∴VE-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| ||
| 3 |
| 4 |
| 3 |
| 2 |
| 8 |
| 27 |
点评:本题考查线面垂直的判定定理与性质定理,考查三棱锥体积的计算,考查学生分析解决问题的能力,难度中等.

练习册系列答案
相关题目
抛物线的顶点在原点,对称轴是x轴,抛物线上点(-5,m)到焦点距离是6,则抛物线的标准方程是( )
| A、y2=-2x |
| B、y2=-4x |
| C、y2=2x |
| D、y2=-4x或y2=-36x |
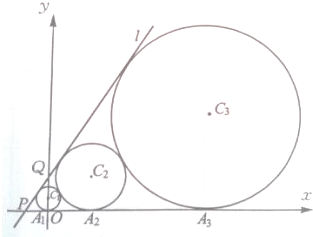 如图,在平面直角坐标系中,直线l经过点P(-1,0),Q(0,
如图,在平面直角坐标系中,直线l经过点P(-1,0),Q(0,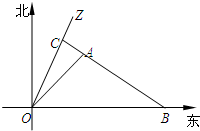 如图所示,一科学考察船从港口O出发,沿北偏东α角的射线OZ方向航行,而在离港口3
如图所示,一科学考察船从港口O出发,沿北偏东α角的射线OZ方向航行,而在离港口3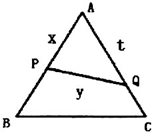 已知△ABC是边长为2的正三角形,P、Q依次是AB、AC边上的点,且线段PQ将△ABC分成面积相等的两部分.设AP=x,AQ=t,PQ=y,求:
已知△ABC是边长为2的正三角形,P、Q依次是AB、AC边上的点,且线段PQ将△ABC分成面积相等的两部分.设AP=x,AQ=t,PQ=y,求: