题目内容
有4个不同的小球，4个不同的盒子，现要把球全部放进盒子内，恰有2个盒子不放球，其有 种方法．（用数字回答）
考点：计数原理的应用
专题：排列组合
分析：先分类，把四个小球先分成两组，每组两个小球，或者是把四个小球分成两组，每组一个和三个，分完小组后再进行排列，从4个盒中选两个位置排列，得到结果．
解答：
解：完成这件事情有两类办法：第一类，一个盒子放3个小球，一个盒子放1个小球，两个盒子不放小球有C41•C43•C31=48种方法；
第二类，有两个盒子各放2个小球，另两个盒子不放小球有C42•C42=36种方法；
由分类计数原理，共有48+36=84种放法．
第二类，有两个盒子各放2个小球，另两个盒子不放小球有C42•C42=36种方法；
由分类计数原理，共有48+36=84种放法．
点评：本题考查分步、分类计数原理，解题的过程中注意这种有条件的排列要分两步走，先选元素再排列．
练习册系列答案
相关题目
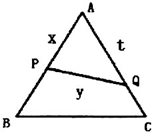已知△ABC是边长为2的正三角形，P、Q依次是AB、AC边上的点，且线段PQ将△ABC分成面积相等的两部分．设AP=x，AQ=t，PQ=y，求：已知i为虚数单位，若复数z=1+i，则|z|的值为（ ）
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |