题目内容
已知集合A={x|x2-3x+2≤0},B={x|(x-1)(x-a)≤0}.
(Ⅰ)若B⊆A,求a的取值范围;
(Ⅱ)若A∩B={1},求a的取值范围.
(Ⅰ)若B⊆A,求a的取值范围;
(Ⅱ)若A∩B={1},求a的取值范围.
考点:集合的包含关系判断及应用,集合关系中的参数取值问题
专题:集合
分析:(I)由x2-3x+2≤0,解得x,即可得到A=[1,2].分类讨论:当a>1时,当a=1时,当a<1时,即可得到集合B.再利用集合之间的关系B⊆A,即可得出.
(II)由A∩B={1},利用(I)即可得出.
(II)由A∩B={1},利用(I)即可得出.
解答:
解:(I)由x2-3x+2≤0,解得1≤x≤2,∴A=[1,2].
当a>1时,B={x|1≤x≤a};
当a=1时,B={1};
当a<1时,B={x|a≤x≤1}.
∵B⊆A,∴1≤a≤2.
因此a的取值范围是[1,2];
(II)∵A∩B={1},由(I)可得:a≤1,
因此a的取值范围是(-∞,1].
当a>1时,B={x|1≤x≤a};
当a=1时,B={1};
当a<1时,B={x|a≤x≤1}.
∵B⊆A,∴1≤a≤2.
因此a的取值范围是[1,2];
(II)∵A∩B={1},由(I)可得:a≤1,
因此a的取值范围是(-∞,1].
点评:本题考查了一元二次不等式的解法、集合之间的关系,考查了分类讨论的思想方法,属于基础题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
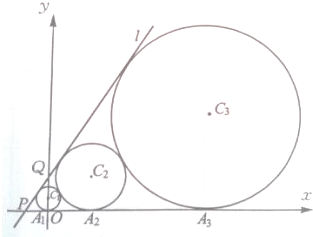 如图,在平面直角坐标系中,直线l经过点P(-1,0),Q(0,
如图,在平面直角坐标系中,直线l经过点P(-1,0),Q(0,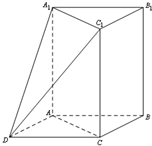 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.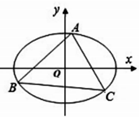 已知椭圆C:
已知椭圆C: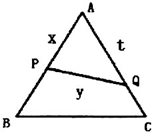 已知△ABC是边长为2的正三角形,P、Q依次是AB、AC边上的点,且线段PQ将△ABC分成面积相等的两部分.设AP=x,AQ=t,PQ=y,求:
已知△ABC是边长为2的正三角形,P、Q依次是AB、AC边上的点,且线段PQ将△ABC分成面积相等的两部分.设AP=x,AQ=t,PQ=y,求: