题目内容
1.设双曲线C的中心为点O,若有且只有一对相交于点O、所成的角为60°的直线A1B1和A${2}_{\;}^{\;}$B2,使|A1B1|=|A${2}_{\;}^{\;}$B2|,其中A1、B1和A2、B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是$(\frac{{2\sqrt{3}}}{3},2]$.分析 先设出双曲线的方程,并根据题意画出图象,根据对称性和条件判断出双曲线的渐近线斜率的范围,列出不等式并转化为关于离心率的不等式,再求解即可.
解答 解:不妨设双曲线的方程是$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),
由|A1B1|=|A2B2|及双曲线的对称性知A1,A2,B1,B2关于x轴对称,如图,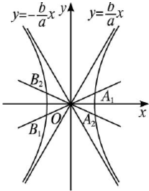
又∵满足条件的直线只有一对,
当直线与x轴夹角为30°时,双曲线的渐近线与x轴夹角大于30°,
双曲线与直线才能有交点A1,A2,B1,B2,
若双曲线的渐近线与x轴夹角等于30°,则无交点,
且不可能存在|A1B1|=|A2B2|,
当直线与x轴夹角为60°时,双曲线渐近线与x轴夹角小于60°,
双曲线与直线有一对交点A1,A2,B1,B2,
若双曲线的渐近线与x轴夹角等于60°,也满足题中有一对直线,
但是如果大于60°,则有两对直线.不符合题意,
∴tan30°<$\frac{b}{a}$≤tan60°,则$\frac{1}{3}<\frac{{b}^{2}}{{a}^{2}}≤3$,
∵b2=c2-a2,∴$\frac{1}{3}<\frac{{c}^{2}-{a}^{2}}{{a}^{2}}≤3$,
解得e∈$(\frac{{2\sqrt{3}}}{3},2]$.
故答案为$(\frac{{2\sqrt{3}}}{3},2]$.
点评 本题考查双曲线的简单性质以及应用,考查数形结合思想和分类讨论思想,属于中档题.

练习册系列答案
相关题目
18.设U=R,A={x|2x<1},B={x|log2x<0},则B∩(∁UA)=( )
| A. | {x|x<0} | B. | {x|x>1} | C. | {x|0<x<1} | D. | {x|0<x≤1} |
6.已知动点P在曲线2x2-y=0上移动,则点A(0,-1)与点P连线中点的轨迹方程是( )
| A. | y=2x2 | B. | y=8x2 | C. | $y=4{x^2}+\frac{1}{2}$ | D. | $y=4{x^2}-\frac{1}{2}$ |
11.下列命题正确的是( )
| A. | 若a>b,则ac2>bc2 | B. | 若a>b>0,c>d>0,则$\frac{a}{d}>\frac{b}{c}$ | ||
| C. | 若a<b<0,则ab<b2 | D. | 若$\frac{a}{b}>1$,则a>b |
 如图所示,直三棱柱ABC-A1B1C1中,AC=3,AB=BB1=4,BC=5,D为BC的中点.
如图所示,直三棱柱ABC-A1B1C1中,AC=3,AB=BB1=4,BC=5,D为BC的中点.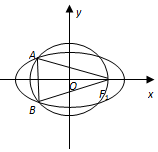 如图,F1是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F1AB是等边三角形,求椭圆的离心率.
如图,F1是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F1AB是等边三角形,求椭圆的离心率.