题目内容

6．已知动点P在曲线2x2-y=0上移动，则点A（0，-1）与点P连线中点的轨迹方程是（　　）
A．y=2x2B．y=8x2C．$y=4{x^2}+\frac{1}{2}$D．$y=4{x^2}-\frac{1}{2}$

分析 先设AP中点为（x，y），进而根据中点的定义可求出P点的坐标，然后代入到曲线方程中得到轨迹方程．

解答 解：设AP中点为（x，y），则P（2x，2y+1）在2x2-y=0上，即2（2x）2-（2y+1）=0，
∴2y=8x2-1，即y=4x2-$\frac{1}{2}$．
故选D．

点评 本题主要考查轨迹方程的求法，正确运用代入法是关键．

练习册系列答案
相关题目
2．已知集合A={x|3≤3x≤27}，B={x|log2x＞1}．
（Ⅰ）求A∩B，A∪B；
（Ⅱ）已知非空集合C={x|1＜x≤a}，若C⊆A，求实数a的取值范围．
3．若函数f（x）=$\frac{（2+m）x}{{x}^{2}-m}$的图象如图所示，则m的范围为（　　）
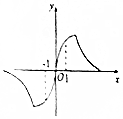
A．（1，+∞）B．（-2，-1）C．（-2，0）D．（-2，1）
14．将一块边长为10的正方形铁片按图1所示的阴影部分裁下，用余下的四个全等的等腰三角形加工成一个底面边长为x的正四棱锥形容器（如图2），则函数f（x）=$\frac{{V}_{E-ABCD}}{x}$的最大值为（　　）
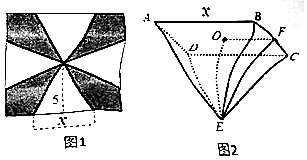
A．$\frac{25\sqrt{3}}{6}$B．$\frac{50}{3}$C．$\frac{25}{3}$D．$\frac{125\sqrt{3}}{6}$
1．设双曲线C的中心为点O，若有且只有一对相交于点O、所成的角为60°的直线A1B1和A${2}_{\;}^{\;}$B2，使|A1B1|=|A${2}_{\;}^{\;}$B2|，其中A1、B1和A2、B2分别是这对直线与双曲线C的交点，则该双曲线的离心率的取值范围是$（\frac{{2\sqrt{3}}}{3}，2]$．
11．已知球面上的四点P、A、B、C，PA、PB、PC的长分别为3、4、5，且这三条线段两两垂直，则这个球的体积为（　　）
A．$\frac{{1000\sqrt{2}}}{3}π$B．$\frac{{375\sqrt{2}}}{16}π$C．50πD．$\frac{{125\sqrt{2}}}{3}π$
18．已知函数f（x）=log${\;}_{\frac{1}{2}}$$\sqrt{-{x}^{2}+2x+8}$．
（1）求f（x）的定义域；
（2）求f（x）的值域．
15．若点A的坐标为（$\frac{1}{2}$，2），F是抛物线y2=2x的焦点，点M在抛物线上移动时，使|MF|+|MA|取得最小值的M的坐标为（$\frac{1}{2}$，1）．
16．设等差数列{an}的前n项和为Sn，若S3=3，S6=15，则a10+a11+a12=（　　）
A．21B．30C．12D．39

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网