题目内容
10.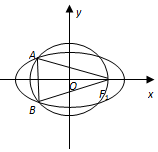 如图,F1是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F1AB是等边三角形,求椭圆的离心率.
如图,F1是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F1AB是等边三角形,求椭圆的离心率.
分析 以O为圆心,以|OF1|为半径的圆的方程为:x2+y2=c2.与椭圆方程联立解得xA,即xD.根据△F1AB是等边三角形,可得∠AOD=60°,因此$\frac{OD}{OA}$=cos60°,解出即可得出.
解答 解:以O为圆心,以|OF1|为半径的圆的方程为:x2+y2=c2.
联立$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}={c}^{2}}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,化为:c2x2=a2(2c2-a2),
解得$x=-\frac{a}{c}$$\sqrt{2{c}^{2}-{a}^{2}}$,
∵△F1AB是等边三角形,(设AB与x轴相交于点D).
∴∠AOD=60°.
∴$\frac{\frac{a}{c}\sqrt{2{c}^{2}-{a}^{2}}}{c}$=cos60°=$\frac{1}{2}$,
化为:e4-8e2+4=0,
解得e2=4-2$\sqrt{3}$,e2=4+2$\sqrt{3}$舍去.
解得e=$\sqrt{3}-1$.
点评 本题考查了椭圆与圆的标准方程及其性质、等边三角形的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知两定点F1(-4,0),F2(4,0),点P是平面上一动点,且|PF1|+|PF2|=9,则点P的轨迹是( )
| A. | 圆 | B. | 直线 | C. | 椭圆 | D. | 线段 |
19.已知点A(-1,0),B(1,0),C(0,1),直线y=kx+b(k≥0)将△ABC分割为面积相等的两部分,则b的取值范围是( )
| A. | (0,1) | B. | $[\frac{1}{3},\frac{1}{2})$ | C. | $[1-\frac{{\sqrt{2}}}{2},\frac{1}{3}]$ | D. | $[1-\frac{{\sqrt{2}}}{2},\frac{1}{2})$ |
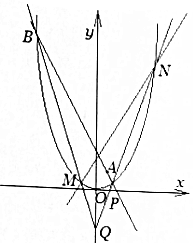 已知过点P($\frac{1}{2}$,0)的直线l与抛物线x2=y交于不同的两点A,B,点Q(0,-1),连接AQ、BQ的直线与抛物线的另一交点分别为N,M,如图所示.
已知过点P($\frac{1}{2}$,0)的直线l与抛物线x2=y交于不同的两点A,B,点Q(0,-1),连接AQ、BQ的直线与抛物线的另一交点分别为N,M,如图所示.