题目内容
18．设U=R，A={x|2x＜1}，B={x|log2x＜0}，则B∩（∁UA）=（ ）| A． | {x|x＜0} | B． | {x|x＞1} | C． | {x|0＜x＜1} | D． | {x|0＜x≤1} |
分析 先分别求出A，B，CUA，由此利用交集定义能求出B∩（∁UA）．
解答 解：∵U=R，A={x|2x＜1}={x|x＜0}，
B={x|log2x＜0}={x|0＜x＜1}，
∴B∩（∁UA）={x|0＜x＜1}∩{x|x≥0}={x|0＜x＜1}．
故选：C．
点评 本题考查补集、交集的求法，是基础题，解题时要认真审题，注意补集、交集的定义的合理运用．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
8．某网站对“爱飞客”飞行大会的日关注量x（万人）与日点赞量y（万次）进行了统计对比，得到表格如下：
由散点图象知，可以用回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$来近似刻画它们之间的关系．
（Ⅰ）求出y关于x的回归直线方程，并预测日关注量为10万人时的日点赞量；
（Ⅱ）一个三口之家参加“爱飞客”亲子游戏，游戏规定：三人依次从装有3个白球和2个红球的箱子中不放回地各摸出一个球，大人摸出每个红球得奖金10元，小孩摸出1个红球得奖金50元．求该三口之家所得奖金总额不低于50元的概率．
参考公式：b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$； 参考数据：$\sum_{i=1}^{5}$xi2=200，$\sum_{i=1}^{5}$xiyi=112．
| x | 3 | 5 | 6 | 7 | 9 |
| y | 2 | 3 | 3 | 4 | 5 |
（Ⅰ）求出y关于x的回归直线方程，并预测日关注量为10万人时的日点赞量；
（Ⅱ）一个三口之家参加“爱飞客”亲子游戏，游戏规定：三人依次从装有3个白球和2个红球的箱子中不放回地各摸出一个球，大人摸出每个红球得奖金10元，小孩摸出1个红球得奖金50元．求该三口之家所得奖金总额不低于50元的概率．
参考公式：b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$； 参考数据：$\sum_{i=1}^{5}$xi2=200，$\sum_{i=1}^{5}$xiyi=112．
13．若a＜b，d＜c，并且（c-a）（c-b）＜0，（d-a）（d-b）＞0，则a、b、c、d的大小关系是（ ）
| A． | d＜a＜c＜b | B． | a＜c＜b＜d | C． | a＜d＜b＜c | D． | a＜d＜c＜b |
3．若函数f（x）=$\frac{（2+m）x}{{x}^{2}-m}$的图象如图所示，则m的范围为（ ）
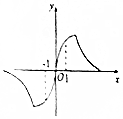
| A． | （1，+∞） | B． | （-2，-1） | C． | （-2，0） | D． | （-2，1） |
4．
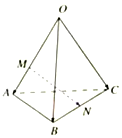如图，空间四边形OABC中，点M、N分别OA、BC上，OM=2MA、BN=CN，则$\overrightarrow{MN}$=（ ）
如图，空间四边形OABC中，点M、N分别OA、BC上，OM=2MA、BN=CN，则$\overrightarrow{MN}$=（ ）| A． | $\frac{1}{2}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | B． | $-\frac{2}{3}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | C． | $\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ | D． | $\frac{2}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ |
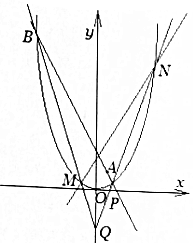已知过点P（$\frac{1}{2}$，0）的直线l与抛物线x2=y交于不同的两点A，B，点Q（0，-1），连接AQ、BQ的直线与抛物线的另一交点分别为N，M，如图所示．