题目内容
13.偶函数f(x)的定义域为R,且在[0,+∞)上是减函数,则f(-$\frac{3}{4}$)≥f(a2-a+1)(填“≥”、“≤”或“>”、“<”或“=”)分析 根据题意,分析可得a2-a+1=(a-$\frac{1}{2}$)2+$\frac{3}{4}$≥$\frac{3}{4}$,结合函数在[0,+∞)上是减函数,可得f($\frac{3}{4}$)≤f(a2-a+1),又由函数为偶函数,则有f(-$\frac{3}{4}$)=f($\frac{3}{4}$),综合可得f(-$\frac{3}{4}$)≤f(a2-a+1),即可得答案.
解答 解:根据题意,a2-a+1=(a-$\frac{1}{2}$)2+$\frac{3}{4}$≥$\frac{3}{4}$,
由函数在[0,+∞)上是减函数,则有f($\frac{3}{4}$)≥f(a2-a+1)
又由f(x)为R上的偶函数,则f(-$\frac{3}{4}$)=f($\frac{3}{4}$)
则有f(-$\frac{3}{4}$)≥f(a2-a+1)
故答案为:≥.
点评 本题考查函数的奇偶性与单调性的综合运用,涉及代数式的大小比较,关键是比较(a2-a+1)的大小.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
4.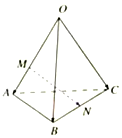 如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )
 如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )| A. | $\frac{1}{2}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | B. | $-\frac{2}{3}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | C. | $\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ | D. | $\frac{2}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ |
5.已知两定点F1(-4,0),F2(4,0),点P是平面上一动点,且|PF1|+|PF2|=9,则点P的轨迹是( )
| A. | 圆 | B. | 直线 | C. | 椭圆 | D. | 线段 |
3.若0<x1<x2<1,则( )
| A. | ${x_2}{e^{x_1}}>{x_1}{e^{x_2}}$ | B. | ${x_2}{e^{x_1}}<{x_1}{e^{x_2}}$ | ||
| C. | lnx2-lnx1>2x2-2x1 | D. | lnx2-lnx1<2x2-2x1 |
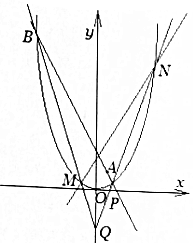 已知过点P($\frac{1}{2}$,0)的直线l与抛物线x2=y交于不同的两点A,B,点Q(0,-1),连接AQ、BQ的直线与抛物线的另一交点分别为N,M,如图所示.
已知过点P($\frac{1}{2}$,0)的直线l与抛物线x2=y交于不同的两点A,B,点Q(0,-1),连接AQ、BQ的直线与抛物线的另一交点分别为N,M,如图所示.