求证:$\frac{1-2sinxcosx}{co{s}^{2}x-si{n}^{2}x}$=$\frac{1-tanx}{1+tanx}$.并证明．题目和参考答案——青夏教育精英家教网—

题目内容

16．求证：$\frac{1-2sinxcosx}{co{s}^{2}x-si{n}^{2}x}$=$\frac{1-tanx}{1+tanx}$，并证明．

分析利用同角三角函数基本关系式化简左边等于右边即可得证．

解答证明：左边=$\frac{si{n}^{2}x+co{s}^{2}x-2sinxcosx}{（cosx+sinx）（cosx-sinx）}$=$\frac{（cosx-sinx）^{2}}{（cosx+sinx）（cosx-sinx）}$=$\frac{cosx-sinx}{cosx+sinx}$=$\frac{1-tanx}{1+tanx}$=右边．
得证．

点评本题主要考查了同角三角函数基本关系式在三角函数证明中的应用，属于基础题．

练习册系列答案

13．若a＜b，d＜c，并且（c-a）（c-b）＜0，（d-a）（d-b）＞0，则a、b、c、d的大小关系是（　　）

4．

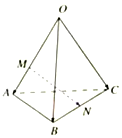如图，空间四边形OABC中，点M、N分别OA、BC上，OM=2MA、BN=CN，则$\overrightarrow{MN}$=（　　）

A．

$\frac{1}{2}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$

B．

$-\frac{2}{3}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$

C．

$\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$

D．

$\frac{2}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$

11．若方程x²+（m-3）x+m=0，m∈R，在x∈R上有两个不相等的实数根，求m的取值范围．

1．设双曲线C的中心为点O，若有且只有一对相交于点O、所成的角为60°的直线A₁B₁和A${2}_{\;}^{\;}$B₂，使|A₁B₁|=|A${2}_{\;}^{\;}$B₂|，其中A₁、B₁和A₂、B₂分别是这对直线与双曲线C的交点，则该双曲线的离心率的取值范围是$（\frac{{2\sqrt{3}}}{3}，2]$．

8．已知直线l₁：x-y+5=0和l₂：x+4=0，抛物线C：y²=16x，P是C上一动点，则P到l₁与l₂距离之和的最小值为$\frac{{9\sqrt{2}}}{2}$..

5．已知两定点F₁（-4，0），F₂（4，0），点P是平面上一动点，且|PF₁|+|PF₂|=9，则点P的轨迹是（　　）

6．已知函数f（x）=（x²+$\frac{3}{2}$）（x+a）（a∈R）．
（Ⅰ）若函数f（x）的图象上有与x轴平行的切线，求a的范围；
（Ⅱ）若f′（-1）=0．证明：对任意的x₁，x₂∈，不等式|f（x₁）-f（x₂）|≤$\frac{5}{16}$恒成立．

试题分类