题目内容
9. 如图所示,直三棱柱ABC-A1B1C1中,AC=3,AB=BB1=4,BC=5,D为BC的中点.
如图所示,直三棱柱ABC-A1B1C1中,AC=3,AB=BB1=4,BC=5,D为BC的中点.(1)求证:AB⊥A1C;
(2)求证:A1C∥平面AB1D;
(3)求三棱锥B1-ABD的体积.
分析 (1)推导出AB⊥AA1,AB⊥AC,从而AB⊥平面ACC1A1,由此能证明AB⊥A1C.
(2)连结AB1,A1B,交于点O,连结OD,推导出OD∥A1C,由此能证明A1C∥平面AB1D.
(3)由BB1⊥平面ABD,${S}_{△ABD}=\frac{1}{2}{S}_{△ABC}$,能求出三棱锥B1-ABD的体积.
解答 证明:(1)∵直三棱柱ABC-A1B1C1中,AA1⊥底面ABC,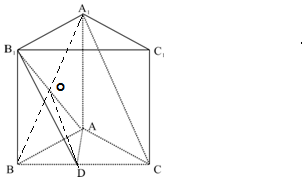
∴AB⊥AA1,
∵AC=3,AB=BB1=4,BC=5,∴AC2+AB2=BC2,∴AB⊥AC,
∵AA1∩AC=A,∴AB⊥平面ACC1A1,
∵A1C?平面ACC1A1,∴AB⊥A1C.
(2)连结AB1,A1B,交于点O,连结OD,
∵直三棱柱ABC-A1B1C1中,BAA1B1是矩形,∴O是A1B的中点,
∵D为BC的中点,∴OD∥A1C,
∵OD?平面AB1D,A1C?平面AB1D,
∴A1C∥平面AB1D.
解:(3)∵BB1⊥平面ABD,${S}_{△ABD}=\frac{1}{2}{S}_{△ABC}$=$\frac{1}{2}×\frac{1}{2}×4×3$=3,
∴三棱锥B1-ABD的体积V=$\frac{1}{3}×B{B}_{1}×{S}_{△ABD}$=$\frac{1}{3}×4×3$=4.
点评 本题考查线线垂直的证明,考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.若函数f(x)=$\frac{(2+m)x}{{x}^{2}-m}$的图象如图所示,则m的范围为( )
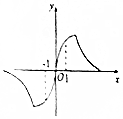

| A. | (1,+∞) | B. | (-2,-1) | C. | (-2,0) | D. | (-2,1) |
4.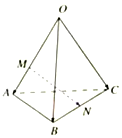 如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )
 如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )
如图,空间四边形OABC中,点M、N分别OA、BC上,OM=2MA、BN=CN,则$\overrightarrow{MN}$=( )| A. | $\frac{1}{2}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | B. | $-\frac{2}{3}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{2}\overrightarrow{OC}$ | C. | $\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ | D. | $\frac{2}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}-\frac{1}{2}\overrightarrow{OC}$ |
14.将一块边长为10的正方形铁片按图1所示的阴影部分裁下,用余下的四个全等的等腰三角形加工成一个底面边长为x的正四棱锥形容器(如图2),则函数f(x)=$\frac{{V}_{E-ABCD}}{x}$的最大值为( )
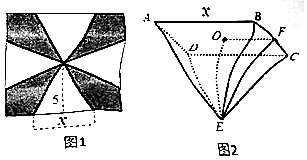

| A. | $\frac{25\sqrt{3}}{6}$ | B. | $\frac{50}{3}$ | C. | $\frac{25}{3}$ | D. | $\frac{125\sqrt{3}}{6}$ |
19.已知点A(-1,0),B(1,0),C(0,1),直线y=kx+b(k≥0)将△ABC分割为面积相等的两部分,则b的取值范围是( )
| A. | (0,1) | B. | $[\frac{1}{3},\frac{1}{2})$ | C. | $[1-\frac{{\sqrt{2}}}{2},\frac{1}{3}]$ | D. | $[1-\frac{{\sqrt{2}}}{2},\frac{1}{2})$ |
 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,G分别是PA,PB,BC的中点;
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,G分别是PA,PB,BC的中点;